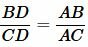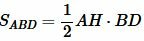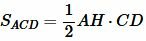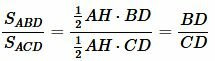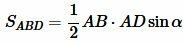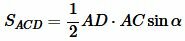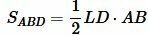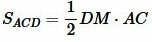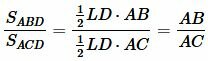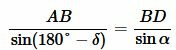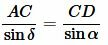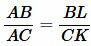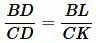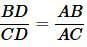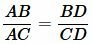Биссектриса делит угол по полам

Обновлено: 11.05.2024

Определение и свойства биссектрисы угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Содержание скрыть

Определение биссектрисы угла треугольника
Свойства биссектрисы треугольника
- Свойство 1 (теорема о биссектрисе)
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

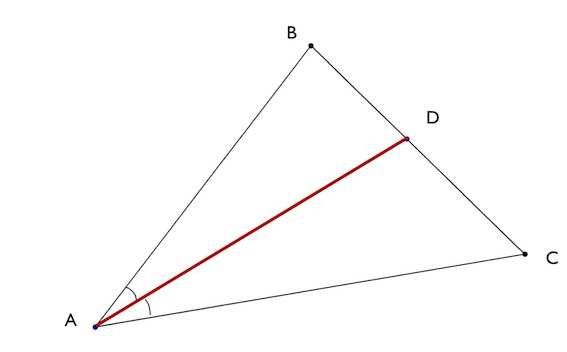
Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.
- СD – внешняя биссектриса угла, смежного с ∠ACB;
- α = β.
Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.
- CD – внутренняя биссектриса ∠ACB;
- CE – биссектриса угла, смежного с ∠ACB;
- ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.
Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

Элементы треугольника. Биссектриса

Свойства биссектрисы

1. Биссектриса треугольника делит угол пополам.

2. Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон ()

3. Точки биссектрисы угла треугольника равноудалены от сторон этого угла.

4. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.

Некоторые формулы, связанные с биссектрисой треугольника

(доказательство формулы – здесь)
, где
— длина биссектрисы, проведённой к стороне ,
— стороны треугольника против вершин соответственно,
— длины отрезков, на которые биссектриса делит сторону ,

Приглашаю посмотреть видеоурок, в котором демонстрируется применение всех указанных выше свойств биссектрисы.

Возможно, вам будет интересен и этот небольшой видеоурок, где применяется одно из свойств биссектрисы

Свойство биссектрисы треугольника

Это важнейшая теорема, о которой можно сказать: в учебнике нет, а на экзамене есть!
Конечно, в учебнике тоже есть. Хорошо спрятанная и никак не выделенная.

Не путать с определением биссектрисы!
Мы помним, что биссектриса – это крыса, которая бегает по углам и делит угол пополам : -)
Теперь серьезно. Биссектриса угла треугольника - это луч, который соединяет вершину треугольника с противоположной стороной, при этом разделяя угол пополам. Это определение биссектрисы.

А вот утверждение о том, что биссектриса угла треугольника делит противолежащую сторону в отношении длин прилежащих сторон, - свойство биссектрисы.

Пусть СР – биссектриса угла ВСА треугольника АВС. Покажем, что

Проведем АD параллельно ВС.

Углы ВСР и АDP равны как накрест лежащие. Значит, треугольники ВРС и АРD подобны по двум углам и Треугольник АСD – равнобедренный, так как углы АСD и СDА равны. Значит, Свойство биссектрисы доказано.

Биссектриса угла (ЕГЭ – 2022)

Когда-то древние астрономы и математики открыли очень много интересных свойств биссектрисы угла треугольников и других фигур.

Эти знания сильно упростили жизнь людей. Стало легче строить, считать расстояния, даже корректировать стрельбу из пушек…

Нам же знание этих свойств поможет решить некоторые задания ЕГЭ!

Биссектриса угла – это геометрическое место точек, равноудаленых от сторон угла.

Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину этого угла с точкой на противолежащей стороне.

Теорема 1. Три биссектрисы в треугольнике пересекаются в одной точке, и эта точка – центр вписанной в треугольник окружности.

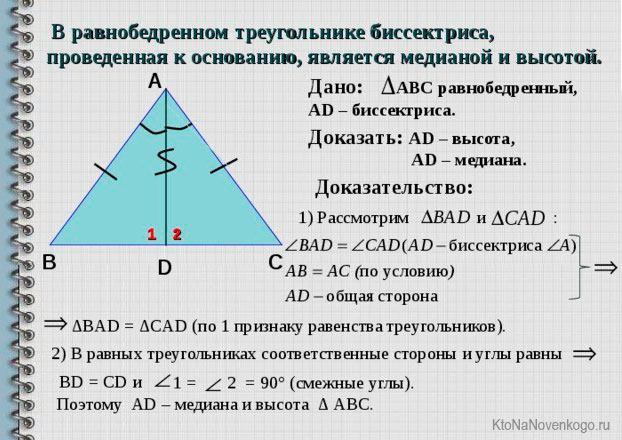
Теорема 2. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.

Теорема 3. Биссектриса угла параллелограмма отсекает равнобедренный треугольник.

Теорема 4. Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.

Теорема 5. Биссектрисы односторонних углов параллелограмма и трапеции пересекаются под прямым углом.

Теорема 6. Отношение отрезков, на которые биссектриса делит противоположную сторону, такое же, как и отношение двух сторон, между которыми эта биссектриса прошла.

Определение биссектрисы угла

Биссектриса угла – это линия, делящая угол пополам.

Или еще вот такое определение биссектрисы:

Биссектриса угла – это геометрическое место точек, равноудаленых от сторон угла.

А вот определение биссектрисы треугольника:

Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину этого угла с точкой на противолежащей стороне.

Тебе встретилась в задаче биссектриса? Постарайся применить одно (а иногда можешь и несколько) из следующих потрясающих свойств.

Биссектриса равнобедренного треугольника

Биссектриса равнобедренного треугольника, проведенная к основанию, является и медианой, и высотой.

Но представляешь, это ещё не всё. Верна ещё и обратная теорема:

Если в треугольнике биссектриса, проведённая из какого-то угла, совпадает с медианой или с высотой, то этот треугольник равнобедренный.

Мы скоро докажем обе этих теоремы, а пока твердо запомни:

Биссектриса совпадает с высотой и медианой только в равнобедренном треугольнике!

Зачем же это твердо запоминать? Как это может помочь?

А вот представь, что у тебя задача:

Дано: \( AB=5,

Найти: \( \displaystyle BC. \)

Ты тут же соображаешь, \(\displaystyle BD \) биссектриса и, о чудо, она разделила сторону \( \displaystyle AC \) пополам! (по условию…).

Если ты твердо помнишь, что так бывает только в равнобедренном треугольнике, то делаешь вывод, что AB=BC и значит, пишешь ответ: BC=5.

Здорово, правда? Конечно, не во всех задачах будет так легко, но знание обязательно поможет!

Доказательство теорем о совпадении биссектрисы с медианой и высотой в равнобедренном треугольнике

Почему в случае с равнобедренным треугольником биссектриса оказывается одновременно и медианой и высотой?

Как это доказать?

Смотри: у \( \triangle ABL \) и \( \triangle CBL \) равны стороны \( AB \) и \( BC \), сторона \( BL \) у них вообще общая и \( \angle 1=\angle 2\). (\( BL \) – биссектриса!)

И вот, получилось, что два треугольника имеют по две равные стороны и угол между ними.

Вспоминаем первый признак равенства треугольников (не помнишь, загляни в тему «Треугольник») и заключаем, что \( \triangle ABL=\triangle CBL \), а значит \( AL \)= \( CL \) и \( \angle 3=\angle 4 \).

\( AL \) = \( CL \) – это уже хорошо – значит, \( BL \) оказалась медианой.

А вот что такое \( \angle 3=\angle 4 \)?

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Кстати, а помнишь ли ты все эти термины? Чем они отличаются друг от друга?

Если нет, не страшно. Сейчас разберемся.
- Основание равнобедренного треугольника – это та сторона, которая не равна никакой другой. Посмотри на рисунок, как ты думаешь, какая это сторона? Правильно – это сторона \( AC. \);
- Медиана – это линия, проведенная из вершины треугольника и делящая противоположную сторону (это снова \( AC \) пополам. Заметь, мы не говорим: «Медиана равнобедренного треугольника». А знаешь почему? Потому что медиана, проведенная из вершины треугольника, делит противоположную сторону пополам в ЛЮБОМ треугольнике.;
- Высота – это линия, проведенная из вершины и перпендикулярная основанию. Ты заметил? Мы опять говорим о любом треугольнике, а не только о равнобедренном. Высота в ЛЮБОМ треугольнике всегда перпендикулярна основанию.
Чем биссектриса, медиана и высота похожи между собой?

Биссектриса, медиана и высота – все они «выходят» из вершины треугольника и упираются в противоположную сторону и «что-то делают» либо с углом из которого выходят, либо с противоположной стороной.

Чем биссектриса, медиана и высота отличаются между собой?
- Биссектриса делит угол, из которого выходит, пополам.
- Медиана делит противоположную сторону пополам.
- Высота всегда перпендикулярна противоположной стороне.
Угол между биссектрисами любого треугольника

B \( \triangle ABC \)проведем две биссектрисы \( AO \)и \( OC \).

Они пересеклись. Какой же угол получился у точки \( O \)?

Давай его посчитаем. Ты помнишь, что сумма углов треугольника равна \( 180<>^\circ \) ?

Применим этот потрясающий факт. С одной стороны, из \( \triangle ABC \):

\( \angle A+\angle B+\angle C=180<>^\circ \), то есть \( \angle B=180<>^\circ \text< >-\text< >\left( \angle A+\angle C \right) \).

Теперь посмотрим на \( \triangle AOC \):

\( \angle 2+\angle 6+\angle 3=180<>^\circ \)

Но биссектрисы, биссектрисы же!

Значит \( \left( \triangle AOC \right) \)

Вспомним про \( \triangle ABC : \angle A+\angle C=180<>^\circ -\angle B \)

Значит, \( \angle 6=180<>^\circ -\frac^\circ -\angle B>=90+\frac \)

Теперь через буквы

Не удивительно ли?

Получилось, что угол между биссектрисами двух углов зависит только от третьего угла!

Ну вот, две биссектрисы мы посмотрели. А что, если их три?! Пересекутся ли они все в одной точке?

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Биссектриса угла – геометрическое место точек, равноудалённых от сторон угла

Ленивые математики как обычно в двух строчках спрятали четыре.

Итак, что же значит, «Биссектриса – геометрическое место точек»? А это значит, что выполняются сразу два утверждения:
1. Если точка лежит на биссектрисе, то расстояния от неё до сторон угла равны.
2. Если у какой-нибудь точки расстояния до сторон угла равны, то эта точка обязательно лежит на биссектрисе.
Почему же верно 1?

Возьмём любую точку на биссектрисе и назовём её \( \displaystyle A. \)

Опустим из этой точки перпендикуляры \( \displaystyle \) AB и \( \displaystyle AC \) на стороны угла.

Итак… Два прямоугольных треугольника: \( \displaystyle AOC \) и \( \displaystyle AOB. \) У них:

Биссектриса треугольника

Напомним, что биссектрисой угла называют луч, делящий угол пополам.

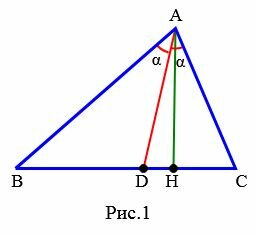
Определение . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника и соединяющий вершину треугольника с точкой на противоположной стороне (рис 1).

Поскольку в каждом треугольнике имеются три угла, то в каждом треугольнике можно провести три биссектрисы.

На рисунке 1 биссектрисой является отрезок AD .

Теорема 1 . Биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.

Доказательство . Продолжим сторону AC треугольника ABC , изображенного на рисунке 1, за точку A . Проведем через точку B прямую, параллельную биссектрисе AD . Обозначим точку пересечения построенных прямых буквой E (рис. 2).

Докажем, что отрезки AB и AE равны. Для этого заметим, что угол EBA равен углу BAD , поскольку эти углы являются внутренними накрест лежащими при параллельных прямых EB и AD . Заметим также, что угол BEA равен углу DAC , поскольку эти углы являются соответственными при параллельных прямых EB и AD . Таким образом, угол EBA равен углу BEA , откуда вытекает, что треугольник EAB является равнобедренным, и отрезки AB и AE равны.

Отсюда, воспользовавшись теоремой Фалеса, получаем:

что и требовалось доказать.

Следствие 1 . Рассмотрим рисунок 3, на котором изображен тот же треугольник, как и на рисунке 1, но для длин отрезков использованы обозначения

b = |AC|, a = |BC|, c = |AB|, p = |BD|, q = |DC|.

что и требовалось доказать.

Следствие 2 . Рассмотрим рисунок 4, на котором изображены две биссектрисы треугольника, пересекающиеся в точке O .

Тогда справедлива формула:

что и требовалось доказать.

Теорема 2 . Рассмотрим рисунок 5, который практически совпадает с рисунком 2.

Тогда для длины биссектрисы справедлива формула:

Доказательство . Из рисунка 5 следует формула

Если воспользоваться этой формулой, то из подобия треугольников ADC и EBC , получаем:

что и требовалось доказать.

Теорема 3 . Длину биссектрисы треугольника (рис.6) можно найти по формуле:

Биссектриса — это луч разрезающий угол пополам, а также отрезок в треугольнике обладающий рядом свойств

Это понятие широко применяется в геометрии. И каждый школьник в России знакомится с ним уже в 5 классе. А после эта величина часто используется для решения различных задач.

Биссектриса — это.

Биссектриса – это луч, который выходит из вершины треугольника и делит ее ровно на две части.

Также под биссектрисой принято понимать и длину отрезка (что это?), который начинается в вершине треугольника, а заканчивается на противоположной от этой вершины стороне.

Есть еще понятие «биссектриса угла», которая является лучом и точно так же делит угол (любой, не обязательно треугольника) пополам:

Само понятие БИССЕКТРИСА пришло к нам из латинского языка. И название это весьма говорящее. Оно состоит из двух слов – «bi» означает «двойное, пара», а «sectio» можно дословно перевести, как «разрезать, поделить».

Вот и получается, что само слово БИССЕКТРИСА – это «разрезание пополам», что собственно и отражается в определении термина, который мы только что привели.

А сейчас задачка на закрепление материала. Посмотрите на эти рисунки и скажите, на каком изображена биссектриса. Подумали? Правильно, на втором.

На первом луч, выходящий из угла АОВ, явно не делит его пополам. На втором это соотношение углов более очевидно, а потому можно предположить, что луч ОД является БИССЕКТРИСОЙ. Хотя, конечно, на сто процентов это утверждать сложно.

Для более точного определения используют специальные инструменты. Например, транспортир. Это такой инструмент в виде полусферы из металла или пластмассы. Вот как он выглядит:

Хотя есть еще вот такие варианты:

Наверняка у каждого такие были в школе. И пользоваться ими весьма просто. Надо только ровненько совместить основание транспортира (прямоугольная линейка) с основанием треугольника, а после на полусфере отметить значение, которое соответствует размеру угла.

И точно по такой же схеме можно поступить наоборот – имея транспортир, начертить угол необходимого размера. Чаще всего – от 0 до 180 градусов. Но на втором рисунке у нас транспортир, который помогает начертить градусы от 0 до 360.

Количество биссектрис в треугольнике

Но вернемся к нашей главной теме. И ответим на вопрос – сколько БИССЕКТРИС есть в треугольнике?

Ответ в общем-то логичен, и он заложен в самом названии нашей геометрической фигуры. Треугольник – три угла. А соответственно, и биссектрис в нем будет тоже три – по одной на каждую вершину.

Снова посмотрим на наши рисунки. В данном случае наглядно видно, что у треугольника АВС (именно так в геометрии обозначается эта фигура – по наименованию ее вершин) три БИССЕКТРИСЫ. Это отрезки AD, BE и CF.

На чертежах БИССЕКТРИСЫ обозначатся следующим образом. Видите одинарные выгнутые черточки между отрезками АС /AL1 и АВ/AL1? Так обозначаются углы. А то, что они оба обозначены одинаковыми черточками, говорит о том, что углы равны. А значит, отрезок AL1 является БИССЕКТРИСОЙ.

То же самое относится и к углам между АВ/DL2 и ВС/BL2. Они обозначены одинаковыми двойными черточками. А значит, отрезок BL2 – биссектриса. А углы АС/CL3 и ВС/CL3 обозначены тройными черточками. Соответственно, это показывает, что отрезок CL3 также является биссектрисой.

Пересечение биссектрис треугольника

Как можно было заметить по приведенным выше рисункам, у биссектрис треугольника есть одно важное свойство. А именно:

Биссектрисы треугольника всегда пересекаются в одной точке, называемой инцентром!

Это правило является аксиомой (что это такое?) и не допускает никаких исключений. Другими словами, вот такого быть не может:

Если вы видите такую картину, то перед вами точно не БИССЕКТРИСЫ. Во всяком случае, минимум один отрезок таковой не является. А может и все три.

А есть еще один интересный факт, связанный с пересечением биссектрис треугольника.

Центр пересечения биссектрис в треугольнике является центром окружности, который списан в эту фигуру.

Это свойство биссектрис на самом деле не только выглядит интересно на чертежах. Оно часто помогает в решение сложных задач.

Свойство основания биссектрисы

У каждой БИССЕКТРИСЫ есть основание. Так называют точку пересечения со стороной треугольника. Например, в нашем случае это будет точка К.

И с этим основанием связана одна весьма интересная теорема. Она гласит, что

Биссектриса треугольника делит противоположную сторону, то есть точкой основания, на два отрезка. И их отношение равно отношению двух прилежащих сторон.

Звучит несколько тяжеловато, но на деле выглядит весьма просто. Отношение отрезков на основании биссектрисы – это ВК/КС. А отношение прилежащих сторон – это АВ/АС. И получается, что в нашем случае теорема выглядит вот так:

Интересно, что для данной теоремы будет справедливо и другое утверждение:

Ну, как часто бывает в математике – это правило работает и в обратном направлении. То есть, если вы знаете длины все сторон и их соотношения равны, то можно сделать вывод, что перед нами БИССЕКТРИСА, А соответственно, будет проще рассчитать размер угла треугольника.

Биссектриса равнобедренного треугольника

Для начала напомним, что такое равнобедренный треугольник.

Это такой треугольник, у которого две стороны абсолютно равны (то есть имеет равные «бедра»).

Так вот в таком треугольнике БИССЕКТРИСА имеет весьма интересные свойства.

Она одновременно является еще и медианой (что это?), и высотой.

Эти понятия нам также знакомы по школьному курсу. Но если кто забыл, мы обязательно напомним:
1. Высота – линия, которая выходит из вершины треугольника и опускается на противоположную сторону под прямым углом.
2. Медиана – линия, которая выходит из вершины треугольника, и делит противоположную сторону на две ровные части.
А в равностороннем треугольнике или как его еще называют правильном (у которого все стороны и все углы равны) все три биссектрисы являются высотами и медианами. И плюс ко всему, их длины равны.

Вот и все, что нужно знать о таком понятии, как БИССЕКТРИСА. До новых встреч на страницах нашего блога.

Эта статья относится к рубрикам:

Комментарии и отзывы (3)

«Высота – линия, которая выходит из вершины треугольника и опускается на противоположную сторону под прямым углом.

Медиана – линия, которая выходит из вершины треугольника, и делит противоположную сторону на две ровные части.»

Некорректно, линия бывает разная,а речь здесь идет о прямой, или её порождениях: отрезок и луч.

Математика требует точности. Спасибо.

При ознакомлении с таким теоретическим материалом всегда возникает вопрос, как можно использовать знания о биссектрисе в реальной жизни, за пределами учебного заведения.

Необходимость делать уроки с собственным ребенком в счет не идет. Конечно, такая информация повышает общую эрудицию, но не несет никакой практической нагрузки, а потому надолго не задерживается в памяти.

Никогда не был силен в геометрии, но наука эта очень важна, знаю, потому как не раз приходилось подтягивать свои знания для решения практических задач.

Биссектриса угла. Свойства

Определение 1. Биссектриса угла − это луч, исходящий из вершины угла и делящий этот угол в два равных угла.

Докажем следующую теорему:

Теорема 1. 1) Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. 2) Каждая точка, которая находится внутри угла и равноудалена от сторон угла, лежит на его биссектрисе.

Доказательство. 1) На биссектрисе угла BAC отметим произвольную точку D. Проведем от точки D перпендикуляры DK и DL к прямым AB и AC, соответственно (Рис.1). Докажем, что DK=DL. Рассмотрим прямоугольные треугольники AKD и ALD. Они равны по гипотенузе и острому углу т.е. \( \small ∠1=∠2 \) , AD общая (см. статью Прямоугольный треугольник). Следовательно DK=DL.

2) Пусть точка D лежит внутри угла BAC и равноудалена от его сторон AB и AC. Докажем, что AD является биссектрисей угла BAC (Рис.1). Проведем перпендикуляры DK и DL к прямым AB и AC. Прямоугольные треугольники AKD и ALD равны по катету и гипотенузе. Действительно, гипотенуза AD общая и по условию DK=DL. Но тогда прямоугольные треугольники AKD и ALD равны. Следовательно \( \small ∠1=∠2 \). А это означает, что луч AD является биссектрисей угла BAC.

Исходя из теоремы 1, можно дать другое определение биссектрисы:

Определение 2. Биссектриса угла − это геометрическое место точек внути угла, равноудаленных от сторон этого угла.

Свойство 1. Угол между биссекстрисами смежных углов равна 90°.

Доказательство. Даны смежные углы CAB и BAD (Рис.2). Покажем, что \( \small ∠EAF=90° \) или . Действительно:

Теорема о биссектрисе треугольника. Доказательство

Теорема 1. Биссектриса при вершине треугольника делит противоположную сторону на две отрезки, пропорциональные сторонам, прилежащим к данной вершине. То есть если биссектриса при вершине A делит в точке D сторону BC на отрезки BD и CD (Рис.1), то имеет место следующее соотношение:

(1)

Доказательство (метод площадей 1). Из вершины A опущена биссектриса AD. Построим вершину треугольника AH. Найдем площади треугольников ABD и ACD:

, (3)

. (4)

Построим следующее соотношение

. (5)

С другой стороны, площадь треугольников ABD и ACD можно найти используя следующие формулы:

. (6)

. (7)

Построим следующее соотношение используя формулы (6) и (7):

. (8)

Из формул (5) и (8) получим соотношение (1).

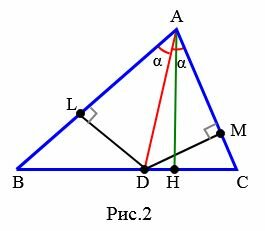
Доказательство (метод площадей 2). С одной стороны, аналогично вышеизложенному имеем соотношение (5). Далее из точки D проведем вершины L и M для треугольников ABD и ACD (Рис.2).

Тогда площади треугольников ABD и ACD можно найти из формул:

, (9)

. (10)

Построим следующее соотношение

. (11)

Из формул (5) и (11) получим соотношение (1).

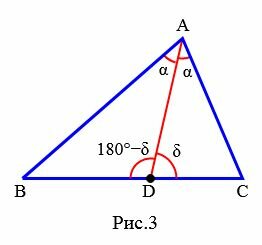
Доказательство (через теорему синусов). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.3):

Применяя теорему синусов для треугольников ABD и ACD можем записать:

, (12)

. (13)

Поделив (12) на (13) и учитывая, что \( \small \sin(180°-\delta)=\sin \delta , \) (см. статью Формулы приведения тригонометрических функций онлайн) получим равенство (1).

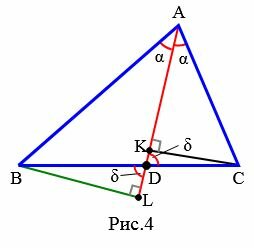
Доказательство (через подобие треугольников). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.4). Проведем перпендикуляры из вершин B и C на луч AD и обозначим точки пересечения через L и K.

Рассмотрим треугольники ABL и ACK. Эти треугольники подобны по двум углам (\( \small ∠ ALB= ∠ AKC ,\;\; ∠ BAL= ∠ CAK \) ). Тогда имеем:

(14)

Рассмотрим, далее, треугольники BLD и CKD. Они также подобны поскольку \( \small ∠ BLD= ∠ CKD ,\) а углы BDL и CDK равны так как они вертикальные. Тогда имеет место следующее соотношение:

(15)

Из равенств (14) и (15) получаем:

.

Пример. Даны стороны треугольника ABC: AB=18, AC=6, BC=20. Найти отрезки, полученные делением биссектрисей большой стороны треугольника.

Решение. Поскольку напротив самой большой стороны треугольника находится вершина A, то бисскетриса AD делит сторону BC на отрезки BD и CD. Тогда имеем:

. (16)

Обозначим BD=x. Тогда CD=BC−x=20−x. Подставляя данные в уравнение (16), получим:

Биссектриса — это крыса, которая бегает по углам и делит угол пополам

Запоминалка, которая помогает запомнить, что такое биссектриса.

Биссектриса (математика, женск.) — прямая линия, проходящая через вершину угла и делящая его пополам.

Применяются и другие запоминалки по математике. Например:

Медиана — обезьяна, она идет по сторонам и делит стороны пополам. (Медиана — прямая линяя, проходящая через вершину и делящая противоположную строну по середине.)

Биссектрисса

Фильм «Всем — спасибо. » (1981 г.)

Фраза "Биссектриса — это крыса, которая бегает по углам и делит угол пополам" упоминается в фильме «Всем — спасибо. » режиссёра Инессы Селезнёвой по сценарию Бориса Золотарёва производства ТО «Экран» (1981 г.). Её произносит Женя (актриса Елена Соловей).

Читайте также: