Квадратные уравнения это фундамент на котором покоится величественное здание алгебры
Обновлено: 17.05.2024
Квадратные уравнения - это фундамент, на котором покоится
Квадратные уравнения - это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. В школьном курсе математики изучают формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Разберём некоторые из них.
Слайд 4 из презентации «Виды квадратных уравнений». Размер архива с презентацией 240 КБ.
Открытый урок с презентацией: "Квадратные уравнения. Виды и способы решения."
план-конспект урока по алгебре (8 класс) на тему

Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Они находят широкое применение при решении различных тригонометрических, показательных, логарифмических, иррациональных, трансцендентных уравнений и неравенств, большого количества разных типов задач.
В школьном курсе математики подробно изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения.
| Вложение | Размер |
|---|---|
| otkrytyy_urok_kvadratnye_uravneniya.doc | 99.5 КБ |
Предварительный просмотр:
Муниципальное казенное общеобразовательное учреждение
средняя общеобразовательная школа №3 с. Чикола
Тема: Квадратные уравнения.
Виды и способы решения.
"Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным".
Макоева Лариса Борисовна
- Усвоить понятие квадратного уравнения, неполного квадратного уравнения.
Получить приемы решения неполных квадратных уравнений.
Уметь находить корни неполных квадратных уравнений. - Развитие вычислительных навыков: навыков решения квадратных уравнений с помощью формул, навыки нахождения дискриминанта квадратного уравнения, развитие логического мышления,
- Способствовать рациональной организации труда, внимательность, активное участие в учебно-познавательном процессе, самостоятельность, самокритичность.
Оборудование к уроку: компьютер, проектор, карточки.
- Организационный момент "Настроимся на урок!" (Знакомство с планом работы на уроке)
- Теоретический опрос на понятие квадратного уравнения. Самостоятельные выводы на вопрос «Каким может быть неполное кв. уравнение?»
- Работа в парах по карточкам: самостоятельно решить предложенные неполные уравнения, с дальнейшей проверкой на доске.
- Историческая справка.
- Фронтальная работа с классом.
- Самостоятельная работа.
- Итог.
1. Организационный момент "Настроимся на урок!" (Слайд 1,2)
Здравствуйте, ребята и гости нашего урока! Математику не зря называют "царицей наук", ей больше, чем какой-либо другой науке, свойственны красота, изящность и точность. Одно из замечательных качеств математики - любознательность. Постараемся доказать это на уроке. Мы с вами начали изучать новый большой раздел «Квадратные уравнения».
Эпиграфом к уроку я взяла слова великого математика Паскаля "Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным". Что перед вами? О каком событии говорят коэффициенты уравнения? (Дата, когда олимпийский огонь будет в нашей республике). ( Слайд 3,4,5)
2. Давайте вспомним. Станция теоретическая. (Слайд 6)
Какой вид имеет квадратное уравнение?
Сколько решений имеет полное квадратное уравнение? От чего это зависит? (Слайд 7)
Ребята, а теперь давайте вместе с вами придем окончательно к выводу: «Какой вид могут иметь неполные квадратные уравнения?» Выслушать мнение ребят, подвести итог. (Слайд 8)
Ученики получают карточки с заданиями. Решают предложенные уравнения, первые называют ответ, далее проверка на экране. (Слайд 9- 11)
- Историческая справка. Станция историческая. (Слайд 12-15)
По словам математика Лейбница, "кто хочет ограничиться настоящим без знания прошлого, тот никогда его не поймет".
Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Они находят широкое применение при решении различных тригонометрических, показательных, логарифмических, иррациональных, трансцендентных уравнений и неравенств, большого количества разных типов задач.
В школьном курсе математики подробно изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. В математической науке есть десять способов решения квадратных уравнений.
Способы решения квадратных уравнений, изучаемые в школе:
- Разложение левой части на множители
- Метод выделения полного квадрата
- С применением формул корней квадратного уравнения
- С применением теоремы Виета
- Графический способ
Продвинутые способы решения квадратных уравнений:
- Способ переброски
- По свойству коэффициентов
- С помощью циркуля и линейки
- С помощью номограммы
- Геометрический
5 Фронтальная работа.
Итак ребята, вы добрались до станции «Тренажерной». Перед тем как приступить к самостоятельной работе поработаем все вместе. (Слайд 16).
- Самостоятельная работа по карточкам.
Учащимся выдаются карточки на два варианта. После выполнения, ответы вводятся на экране. (Слайд 17)
7. Итог урока. Станция «Конечная». (Слайд 18)
Что нового мы узнали на уроке?
Какое уравнение называется квадратным?
Какие виды квадратных уравнений вы знаете?
Момент рефлексии: учащимся предлагается ответить на вопросы:
Что понравилось мне сегодня на уроке?
В чем я испытывал затруднения?
Сегодня мне удалось…
И закончить сегодняшний урок хотелось бы словами великого математика У. Сойера: «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт»
Домашнее задание и номера выполняемые в классе соответствуют учебнику «Алгебра 8», автор С.М. Никольский, М.К. Потапов и др.
Способы решения квадратных уравнений
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения (Приложение 1).
Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Имеется десять способов решения квадратных уравнений. Подробно остановимся на каждом из них.
1 способ: разложение левой части уравнения на множители.
Разложим левую часть на множители:
х2 + 10х - 24 = х2 + 12х - 2х - 24 = х(х + 12) - 2(х + 12) = (х + 12)(х - 2).
Следовательно, уравнение можно переписать так:
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = - 12. Это означает, что число 2 и - 12 являются корнями уравнения х2 + 10х - 24 = 0.
2 способ: метод выделения полного квадрата.
Решим уравнение х2 + 6х - 7 = 0.
Выделим в левой части полный квадрат.
Для этого запишем выражение х2 + 6х в следующем виде:
х2 + 6х = х2 + 2• х • 3.
В полученном выражении первое слагаемое - квадрат числа х, а второе - удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 32, так как х2 + 2• х • 3 + 32 = (х + 3)2.
Преобразуем теперь левую часть уравнения
прибавляя к ней и вычитая 32. Имеем:
х2 + 6х - 7 = х2 + 2• х • 3 + 32 - 32 - 7 = (х + 3)2 - 9 - 7 = (х + 3)2 - 16.
Таким образом, данное уравнение можно записать так:
(х + 3)2 - 16 =0, (х + 3)2 = 16.
Следовательно, х + 3 - 4 = 0, х1 = 1, или х + 3 = -4, х2 = -7.
3 способ: решение квадратных уравнений по формуле.
Умножим обе части уравнения
на 4а и последовательно имеем:
(2ax + b)2 = b2 - 4ac,
Примеры. Сколько корней имеет уравнение?
а) 4х2 + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b2 - 4ac = 72 - 4 • 4 • 3 = 49 - 48 = 1,
D > 0, два разных корня;
Таким образом, в случае положительного дискриминанта, т.е. при
b2 - 4ac >0 , уравнение ах2 + bх + с = 0 имеет два различных корня.
б) 4х2 - 4х + 1 = 0,
а = 4, b = - 4, с = 1, D = b2 - 4ac = (-4)2 - 4 • 4 • 1= 16 - 16 = 0,
D = 0, один корень;
Итак, если дискриминант равен нулю, т.е. b2 - 4ac = 0, то уравнение
ах2 + bх + с = 0 имеет единственный корень,
в) 2х2 + 3х + 4 = 0,
а = 2, b = 3, с = 4, D = b2 - 4ac = 32 - 4 • 2 • 4 = 9 - 32 = - 13 , D < 0.
Данное уравнение корней не имеет.
Итак, если дискриминант отрицателен, т.е. b2 - 4ac < 0,
уравнение ах2 + bх + с = 0 не имеет корней.
Формула (1) корней квадратного уравнения ах2 + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.
4 способ: решение уравнений с использованием теоремы Виета.
Как известно, приведенное квадратное уравнение имеет вид
Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
а) Если сводный член q приведенного уравнения (1) положителен (q > 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р > 0, то оба корня отрицательны, если р < 0, то оба корня положительны.
Например, x2 – 3x + 2 = 0; x1 = 2 иx2 = 1, так какq = 2 > 0 иp = - 3 < 0;
б) Если свободный член q приведенного уравнения (1) отрицателен (q < 0), то имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p < 0 , или отрицателен, если p > 0 .
Пример: x2 + 4x – 5 = 0; x1 = - 5 иx2 = 1, так какq= - 5 < 0 иp = 4 > 0;
5 способ: решение уравнений способом «переброски»( Приложение 2).
Умножая обе его части на а, получаем уравнение
Пусть ах = у, откуда х = у/а; тогда приходим к уравнению
у2 + by + ас = 0, равносильно данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х1 = у1/а и х1 = у2/а.
При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Пример. Решим уравнение 2х2 – 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
Согласно теореме Виета
у1 = 5 х1 = 5/2 x1 = 2,5
6 способ: свойства коэффициентов квадратного уравнения (Приложение 2)
А.Пусть дано квадратное уравнение
1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1
Согласно теореме Виета
По условию а – b + с = 0, откуда b = а + с. Таким образом,
т.е. х1 = -1 и х2 = c/a, что м требовалось доказать.
1) Решим уравнение 345х2 – 137х – 208 = 0.
Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то
2)Решим уравнение 132х2 – 247х + 115 = 0.
Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то
Б. Если второй коэффициент b = 2k – четное число, то формулу корней.
Решим уравнение 3х2 — 14х + 16 = 0.
D = k2 – ac = (- 7)2 – 3 • 16 = 49 – 48 = 1, D > 0, два различных корня;
В. Приведенное уравнение х2 + рх + q= 0 совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней принимает вид:
Формулу (3) особенно удобно использовать, когда р — четное число.
Пример. Решим уравнение х2 – 14х – 15 = 0.
Ответ: х1 = 15; х2 = -1.
7 способ: Графическое решение квадратного уравнения.
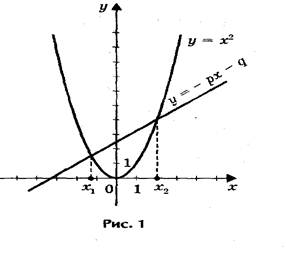
Если в уравнении х2 + px + q = 0 перенести второй и третий члены в правую часть, то получим х2 = - px - q.
Построим графики зависимости у = х2 и у = - px - q.
График первой зависимости - парабола, проходящая через начало координат. График второй зависимости - прямая (рис.1). Все данные вводим в программу«Advanced Grapher» и получаем ответы [13].
Искомая окружность пересекает ось абсцисс в точках B (х1 ;0) и D (х2 ;0), где х1 и х2 – корни уравнения ах2 + bх + с=0, и проходит через точки А (0;1) и С (0; ) на оси ординат. [5, c.34]
- прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
- прямая и парабола могут касаться ( только одна общая точка), т.е. уравнение имеет одно решение;
- прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
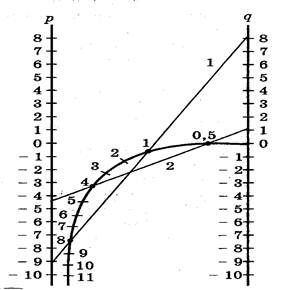
1) Решим графически уравнение х2 - 3х - 4 = 0 (рис. 2).
Решение. Запишем уравнение в виде х2 = 3х + 4.
Построим параболу у = х2 и прямую у = 3х + 4. Прямую у = 3х + 4 можно построить по двум точкам М (0; 4) и N (3; 13). Прямая и парабола пересекаются в двух точках А и В с абсциссами х1 = - 1 и х2 = 4.
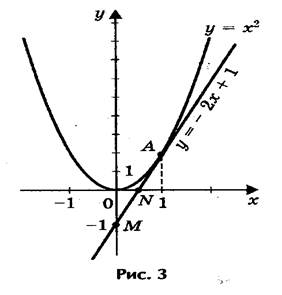
2) Решим графически уравнение (рис. 3) х2 - 2х + 1 = 0.
Решение. Запишем уравнение в виде х2 = 2х - 1.
Построим параболу у = х2 и прямую у = 2х - 1.
Прямую у = 2х - 1 построим по двум точкам М (0; - 1)
и N(1/2; 0). Прямая и парабола пересекаются в точке А с
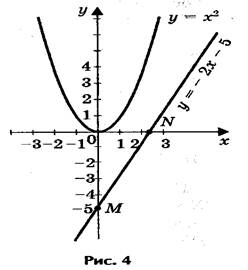
3) Решим графически уравнение х2 - 2х + 5 = 0 (рис. 4).
Решение. Запишем уравнение в виде х2 = 5х - 5. Построим параболу у = х2 и прямую у = 2х - 5. Прямую у = 2х - 5 построим по двум точкам М(0; - 5) и N(2,5; 0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет.
Ответ. Уравнение х2 - 2х + 5 = 0 корней не имеет.
8 способ:: решение квадратных уравнений с помощью циркуля и линейки.
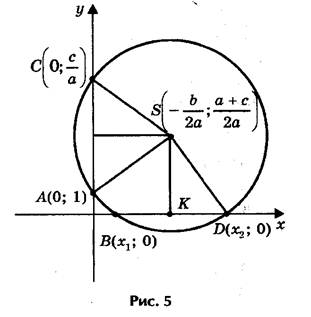
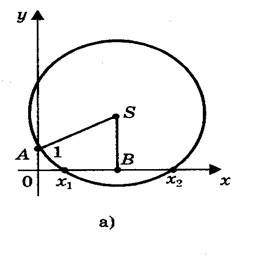
Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика. Найти корни квадратного уравнения ах2 + bх + с = 0 с помощью циркуля и линейки (рис. 5). [5, c.34]
Допустим, что искомая окружность пересекает ось абсцисс в точках В(х1; 0 ) и D (х2; 0), где х1 и х2 - корни уравнения ах2 + bх + с = 0, и проходит через точки А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = OB • OD/ OA= х1х2/ 1 = c/a.
Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD.
Итак: 1) построим точки (центр окружности) и A(0; 1);
2) проведем окружность с радиусом SA;
3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
1) Радиус окружности больше ординаты центра (AS > SK, или R > a + c/2a), окружность пересекает ось Ох в двух точках (рис. 6,а) В(х1; 0) и D(х2; 0), где х1 и х2 - корни квадратного уравнения ах2 + bх + с = 0.
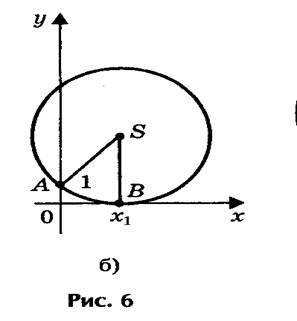
2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис. 6,б) в точке В(х1; 0), где х1 - корень квадратного уравнения.
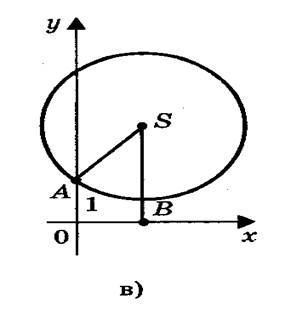
3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс (рис.6,в), в этом случае уравнение не имеет решения.
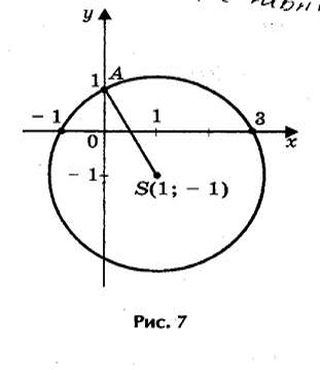
Пример. Решим уравнение х2 - 2х - 3 = 0 (рис. 7).
Решение. Определим координаты точки центра окружности по формулам:
Проведем окружность радиуса SA, где А (0; 1).
9 способ: решение квадратных уравнений с помощью номограммы.
Это старый и незаслуженно забыты способ решения квадратных уравнений, помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. - М., Просвещение, 1990) [ 3, c.83] .
Таблица XXII. Номограмма для решения уравнения z2 + pz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.
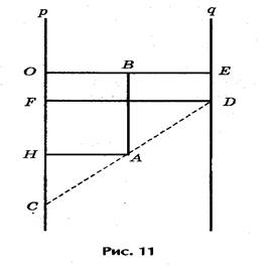
Криволинейная шкала номограммы построена по формулам (рис.11):
Полагая ОС = р, ED = q, ОЕ = а (все в см.), из подобия треугольников САН и CDF получим пропорцию
откуда после подстановок и упрощений вытекает уравнение
причем буква z означает метку любой точки криволинейной шкалы.
1) Для уравнения z2 - 9z + 8 = 0 номограмма дает корниz1 = 8,0 и z2 = 1,0 (рис.12).
2) Решим с помощью номограммы уравнение
Разделим коэффициенты этого уравнения на 2, получим уравнение
Номограмма дает корни z1 = 4 иz2 = 0,5.
3) Для уравнения
коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5t, получим уравнение t2 - 5t + 2,64 = 0, которое решаем посредством номограммы и получим t1 = 0,6 и t2 = 4,4, откудаz1 = 5t1 = 3,0 иz2 = 5t2 = 22,0.
10 способ: геометрический способ решения квадратных уравнений.
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал - Хорезми.
Примеры.
1) Решим уравнение х2 + 10х = 39.
В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.15).
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.
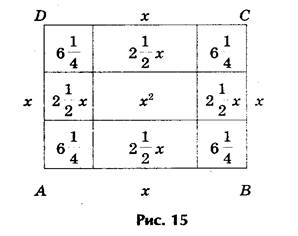
Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х2, четырех прямоугольников (4• 2,5х = 10х ) и четырех пристроенных квадратов (6,25• 4 = 25), т.е. S = х2 + 10х + 25. Заменяя
х2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим
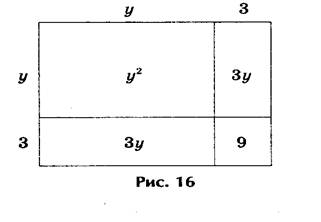
А вот, например, как древние греки решали уравнение у2 + 6у - 16 = 0.
Решение представлено на рис. 16, где у2 + 6у = 16,
или у2 + 6у + 9 = 16 + 9.
Решение. Выражения у2 + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у2 + 6у - 16 + 9 - 9 = 0 - одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у1 = 2, у2 = - 8 (рис.16).
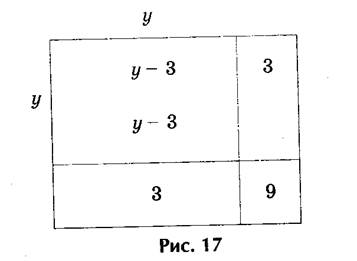
3) Решить геометрически уравнение у2 - 6у - 16 = 0.
Преобразуя уравнение, получаему2 - 6у = 16.
На рис. 17 находим «изображения» выражения у2 - 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у2 - 6у прибавить 9, то получим площадь квадрата со стороной у - 3. Заменяя выражение у2 - 6у равным ему числом 16,
Заключение
Подводя итоги, можно сделать вывод: квадратные уравнения играют огромную роль в развитии математики. Не менее важно и то, что в результате применения квадратных уравнений при решении задач не редко обнаруживаются новые детали, удается сделать интересные обобщения и внести уточнения, которые подсказываются анализом полученных формул и соотношений.
Хочется отметить и то, что излагаемая тема в этой работе еще мало изучена, поэтому она таит в себе много скрытого и неизвестного, что дает прекрасную возможность для дальнейшей работы над ней. Здесь мы остановилась на вопросе решения квадратных уравнений, а что, если существуют и другие способы их решения?! Опять находить красивые закономерности, какие-то факты, уточнения, делать обобщения, открывать все новое и новое.
Но это вопросы уже следующих работ. В результате изучения новых способов решения квадратных уравнений мы получили возможность решать уравнения не только по формуле, но и более интересными способами. Решили множество уравнений, изучили программу «Advanced Grapher». Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи.
Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт. Данная исследовательская работа может быть использована учителями математики на уроках и элективных курсах по математике при изучении темы «Квадратные уравнения» (Приложения 1-3), учениками для расширения и углубления знаний по решению квадратных уравнений. Любой учащийся, используя эту исследовательскую работу, может самостоятельно изучить данную тему (Приложения 1-2).
Теоретический материал по теме "10 способов решений квадратных уравнений"
Квадратные уравнения - это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Многие практические задачи решаются с их помощью. Например, квадратное уравнение позволяет рассчитать тормозной путь автомобиля, мощность ракеты для вывода на орбиту космического корабля, траектории движения различных физических объектов – от элементарных частиц до звёзд.
В школе изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения. Предлагаю 10.
Определение 1. Квадратным уравнением называют уравнение вида ах 2 + b х + с = 0, где коэффициенты а, в, с- действительные числа, а ≠ 0.
Определение 2 . Полное квадратное уравнение — это квадратное уравнение, в котором присутствуют все три слагаемых т.е. коэффициенты в и с отличны от нуля.
Неполное квадратное уравнение — это уравнение, в котором хотя бы один из коэффициентов в или, с равен нулю.
Определение 3. Корнем квадратного уравнения ах 2 + вх + с = 0 называют всякое значение переменной х, при котором квадратный трехчлен ах 2 + вх + с обращается в нуль.
Определение 4 . Решить квадратное уравнение — значит найти все его
корни или установить, что корней нет.
Разложение левой части уравнения на множители.
Решим уравнение х 2 + 10х - 24 = 0 .
Разложим левую часть на множители:
х 2 + 10х - 24 = х 2 + 12х - 2х - 24 = х(х + 12) - 2(х + 12) = (х + 12)(х - 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х - 2) = 0
Произведение множителей равно нулю, если по крайней мере, один из его множителей равен нулю.
х + 12= 0 или х – 2=0
2. Метод выделения полного квадрата двучлена.
Решим уравнение х 2 + 6х - 7 = 0 .
Выделим в левой части полный квадрат:
х 2 + 6х - 7 = х 2 + 2 • х • 3 + 3 2 - 3 2 - 7 = (х + 3) 2 - 9 - 7 = (х + 3) 2 - 16.
тогда, данное уравнение можно записать так:
(х + 3) 2 - 16 =0,
(х + 3) 2 = 16.
х + 3=4 или х + 3 = -4
х 1 = 1 х 2 = -7
3.Решение квадратных уравнений по формулам.
а) Решим уравнение:
4х 2 + 7х + 3 = 0.
а = 4, b = 7, с = 3.
D = b 2 - 4 ac = 7 2 - 4 • 4 • 3 = 49 - 48 = 1, D > 0, уравнение имеет два различных корня;
б) Решим уравнение:
4х 2 - 4х + 1 = 0,
а = 4, b = - 4, с = 1,
D = b 2 - 4 ac = (-4) 2 - 4 • 4 • 1= 16 - 16 = 0, D = 0, уравнение имеет один корень;
в) Решим уравнение: 2х 2 + 3х + 4 = 0,
а = 2, b = 3, с = 4, D = b 2 - 4 ac = 3 2 - 4 • 2 • 4 = 9 - 32 = - 13 , D < 0.
Данное уравнение корней не имеет.
Ответ: корней нет.
4. Решение уравнений с использованием теоремы Виета.
Чтобы квадратное уравнение привести к приведенному виду, нужно все его члены разделить на a ,, тогда
сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
x 2 – 8 x – 9 = 0; x 1 = 9 и x 2 = - 1,
x 2 + 4 x – 5 = 0; x 1 = - 5 и x 2 = 1,
x 2 – 3 x + 2 = 0; x 1 = 2 и x 2 = 1,
x 2 + 8 x + 7 = 0; x 1 = - 7 и x 2 = - 1.
5. Решение уравнений способом «переброски».
Рассмотрим квадратное уравнение
ах 2 + b х + с = 0, где а ≠ 0.
Умножая обе его части на а, получаем уравнение а 2 х 2 + а b х + ас = 0.
Пусть ах = у , откуда х = у/а ; тогда приходим к уравнению у 2 + by + ас = 0,
Его корни у 1 и у 2 найдем с помощью теоремы Виета и окончательно:
х 1 = у 1 /а и х 1 = у 2 /а .
При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски» . Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Решим уравнение 2х 2 – 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у 2 – 11у + 30 = 0.
Согласно теореме Виета
у 1 = 5 , х 1 = 5/2 , x 1 = 2,5
у 2 = 6; x 2 = 6/2; x 2 = 3.
6. Свойства коэффициентов квадратного уравнения.
1. Пусть дано квадратное уравнение ах 2 + b х + с = 0, где а ≠ 0.
Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю),
то х 1 = 1, х 2 = с/а.
Если a – b + c =0, то х 2 =-1, х 2 = -с/а
А. Решим уравнение 345х 2 – 137х – 208 = 0.
Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то
х 1 = 1, х 2 = c / a = -208/345.
Ответ: 1; -208/345.
Б. Решим уравнение 132х 2 – 247х + 115 = 0.
Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то
х 1 = 1, х 2 = c / a = 115/132.
Ответ: 1; 115/132.
2) Решим уравнение 2х 2 + 3х +1= 0. Так как 2 - 3+1=0, значит х 1 = - 1, х 2 = -с/а= -1/2
Данный метод удобно применять к квадратным уравнениям с большими коэффициентами.
2. Если второй коэффициент уравнения b = 2 k – четное число, то формулу корней можно записать в виде
Решим уравнение 3х 2 — 14х + 16 = 0 .
Решение . Имеем: а = 3, b = — 14 ( k = —7), с = 16,
D 1 = k 2 – ac = (- 7) 2 – 3 • 16 = 49 – 48 = 1, D 1 > 0, уравнение имеет два различных корня;

Приведенное уравнение х 2 + рх + q = 0 совпадает с уравнением общего вида, в котором а = 1 , b = р и с = q . Поэтому для приведенного квадратного уравнения формула корней принимает вид
Формулу ( ) удобно использовать, когда р — четное число.
Пример. Решим уравнение х 2 – 14х – 15 = 0.
Решение. Имеем а=1, в =-14, (к=-7),с=-15.
х 1,2 =7± =7 ± ,
х 1,2 = 15; х 2 = -1.
Ответ: х 1 = 15; х 2 = -1.
7.Графическое решение квадратного уравнения.
И спользуя знания о квадратичной и линейной функциях и их графиках, можно решить квадратное уравнение так называемым функционально-графическим методом. Причем некоторые квадратные уравнения можно решить различными способами, рассмотрим эти способы на примере одного квадратного уравнения.
Пример. Решить уравнение =0
1способ . Построим график функции , воспользовавшись алгоритмом.
Значит, вершиной параболы служит точка (1;-4), а осью параболы – прямая x=1
2) Возьмем на оси х две точки, симметричные относительно оси параболы, например точки рис.2
х= -1 и х=3, тогда f (-1)= f (3)=0.
3) Через точки (-1;0) , (1;-4), (3;0) проводим параболу (рис 2).
Корнями уравнений являются абсциссы точек пересечения параболы с осью х; значит, корни уравнения
2 способ
Преобразуем уравнение к виду .
Построим в одной системе координат графики функций и (рис 3 ).
Они пересекаются в двух точках A(-1;1) и B(3;9). Корнями уравнения служат абсциссы точек A и B , значит, .
3 способ
Преобразуем уравнения к виду.
Построим в одной системе координат графики функций и (рис.4) Они пересекаются в двух точках A(-1;-2) и В (3;6). Корнями уравнения являются абсциссы точек А и В, поэтому .
Рис.4
4 способ
Преобразуем уравнение к виду , затем т.е.
Построим в одной системе координат параболу и прямую . Они пересекаются в точках А(-1;4) и В(3;4). Корнями уравнений служат абсциссы точек А и В, поэтому (рис.5) .
5 способ
Разделим почленно обе части уравнения на x, получим:
Построим в одной системе координат гиперболу и прямую (рис.6). Они пересекаются в двух точках А(-1;-3) и В(3;1). Корнями уравнений являются абсциссы точек А и В, следовательно, .
Первые четыре способа применимы к любым уравнениям вида
ах 2 + b х + с = 0, а пятый- только к тем, у которых с не равно нулю.
Графические способы решения квадратных уравнений красивы, но не дают стопроцентной гарантии решения любого квадратного уравнения.
8. Решение квадратных уравнений с помощью циркуля и

Предлагаю следующий способ нахождения корней квадратного уравнения ах 2 + b х + с = 0 с помощью циркуля и линейки (рис.7 ).
Допустим, что искомая окружность пересекает ось
абсцисс в точках В(х 1 ; 0 ) и D (х 2 ; 0), где х 1 и х 2 - корни уравнения ах 2 + b х + с = 0 , и проходит через точки
А(0; 1) и С(0; c / a ) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC , откуда OC = OB • OD / OA = х 1 х 2 / 1 = c / a .
Центр окружности находится в точке пересечения перпендикуляров SF и SK , восстановленных в серединах хорд AC и BD , поэтому

Итак:
1) построим точки (центр окружности) и A (0; 1) ;
2) проведем окружность с радиусом SA ;
3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
1) Радиус окружности больше ординаты центра ( AS > SK , или R > a + c /2 a ) , окружность пересекает ось Ох в двух точках (рис. 8а) В(х 1 ; 0) и D (х 2 ; 0) , где х 1 и х 2 - корни квадратного уравнения ах 2 + b х + с = 0 .
2) Радиус окружности равен ординате центра ( AS = SB , или R = a + c /2 a ) , окружность касается оси Ох (рис.8б) в точке В(х 1 ; 0) , где х 1 - корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра
окружность не имеет общих точек с осью абсцисс (рис 8в), в этом случае уравнение не имеет решения.
Решим уравнение х 2 - 2х - 3 = 0 (рис.9).
Решение. Определим координаты точки центра окружности по формулам:

Проведем окружность радиуса SA , где А (0; 1).
Ответ: х 1 = - 1; х 2 = 3.
9. Решение квадратных уравнений с помощью
Это старый и в настоящее время забытый способ решения квадратных уравнений, помещенный на с.83 сборника: Брадис В.М. Четырехзначные математические таблицы. - М., Просвещение, 1990.
Таблица XXII . Номограмма для решения уравнения z 2 + pz + q = 0 . Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициен-
там определить корни уравнения.
Криволинейная шкала номограммы построена
по формулам (рис.10):
![]()
Полагая ОС = р, ED = q , ОЕ = а (все в см.), из
подобия треугольников САН и CDF получим
откуда после подстановок и упрощений вытекает уравнение
z 2 + pz + q = 0,
причем буква z означает метку любой точки криволинейной шкалы.
1) Для уравнения z 2 - 9 z + 8 = 0 номограмма дает корни z 1 = 8,0 и z 2 = 1,0 (рис. 11).
Ответ: 8,0 ; 1,0.
2) Решим с помощью номограммы уравнение
2 z 2 - 9 z + 2 = 0.
Разделим коэффициенты этого уравнения на 2,
получим уравнение z 2 - 4,5 z + 1 = 0.
Номограмма дает корни z 1 = 4 и z 2 = 0,5.
3) Для уравнения z 2 - 25 z + 66 = 0 коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5 t , получим уравнение t 2 - 5 t + 2,64 = 0,
которое решаем посредством номограммы и получим t 1 = 0,6 и t 2 = 4,4, откуда z 1 = 5 t 1 = 3,0 и z 2 = 5 t 2 = 22,0.
10. Геометрический способ решения квадратных уравнений.
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал - Хорезми.
1) Решим уравнение х 2 + 10х = 39.
В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.12).
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD , достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.

Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х 2 , четырех прямоугольников (4• 2,5х = 10х ) и четырех пристроенных квадратов (6,25• 4 = 25) , т.е. S = х 2 + 10х + 25. Заменяя
х 2 + 10х числом 39 , получим, что S = 39 + 25 = 64 , откуда следует, что сторона квадрата ABCD , т.е. отрезок АВ = 8 . Для искомой стороны х первоначального квадрата получим

2) А вот, например, как древние греки решали уравнение у 2 + 6у - 16 = 0 .
Решение представлено на рис 13. где
у 2 + 6у = 16, или у 2 + 6у + 9 = 16 + 9.
Решение. Выражения у 2 + 6у + 9 и 16 + 9 геометрически представляют собой
один и тот же квадрат, а исходное уравнение у 2 + 6у - 16 + 9 - 9 = 0 - одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у 1 = 2, у 2 = - 8 (рис. .
3) Решить геометрически уравнение у 2 - 6у - 16 = 0.
Преобразуя уравнение, получаем
у 2 - 6у = 16.
На рис 14. находим «изображения» выражения у 2 - 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3 . Значит, если к выражению у 2 - 6у прибавить 9 , то получим площадь квадрата со стороной у - 3 . Заменяя выражение у 2 - 6у равным ему числом 16,
получаем: (у - 3) 2 = 16 + 9, т.е. у - 3 = ± √25 , или у - 3 = ± 5, где у 1 = 8 и у 2 = - 2.
Квадратные уравнения Квадратные уравнения- это фундамент, на котором покоиться величественное здание алгебры. - презентация
Презентация на тему: " Квадратные уравнения Квадратные уравнения- это фундамент, на котором покоиться величественное здание алгебры." — Транскрипт:
1 Квадратные уравнения Квадратные уравнения- это фундамент, на котором покоиться величественное здание алгебры
2 Способы решения квадратных уравнений
3 Разложение на множители
4 Выделение полного квадрата
5 Алгоритм решения квадратного уравнения Квадратное уравнение Общая формула Общая формула с четным коэффициентом Теорема Виета
7 Общая формула с четным коэффициентом
8 Теорема Виета (прямая и обратная)
9 Теорема Виета (прямая и обратная
13 Свойства коэффициентов квадратного уравнения УравненияСвойства Коэффициентов Корни
17 Способы решения Геометрический С помощью номограммы С помощью циркуля и линейки
18 С помощью номограммы
19 Пример1. Ответ : 1; 8. Ответ: 0,5; 4. Пример2.
22 С помощью циркуля и линейки
23 построим точки S (центр окружности) и А(0;1); проведем окружность с радиусом SA; абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
24 При этом возможны три случая. 1) Радиус окружности больше ординаты центра окружность пересекает ось Ох в двух точках (рис.6,а) В(х1;0) и D(х2;0), где х1 и х2 – корни квадратного уравнения 2) Радиус окружности равен ординате центра окружность касается оси Ох (рис.6,б) в точке В(х1;0), где х1 – корень квадратного уравнения. 3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс (рис.6,в), в этом случае уравнение не имеет решения.
Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, - презентация
2 Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, иррациональных уравнений и неравенств. В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения.
4 Основополагающий вопрос Почему нам нужны уравнения? Проблемные вопросы учебной темы Какие способы решения уравнений вы знаете? Учебные вопросы по содержанию Что такое квадратное уравнение? Как найти корни квадратного уравнения? Где применяют квадратные уравнения? Какие способы решения квадратных уравнений вы знаете? Что такое теорема Виета? Как она применяется?
5 Когда научились решать квадратные уравнения? Виды и общие методы решения квадратных уравнений. Специальные методы решения квадратных уравнений. Всегда ли возможно решение квадратных уравнений? Теорема Виета и ее применение Вопросы для исследования
7 Защита полученных результатов и выводов. Решение заданий и выполнение тестов. Урок-игра.
8 Знаю-интересуюсь-учусь Что я знаю?Чем я интересуюсь? Что я узнал? Что такое уравнение. Что такое квадратное уравнение? Как его решать? Способы решения уравнений. Теорема Виета. Формула корней квадратного уравнения. Способы решения уравнений.
9 Формы представления результатов Презентация Буклет Публикация
10 Сроки реализации проекта 2 месяца
11 «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу различными способами, чем решать три- четыре различные задачи. Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт». У. У. Сойер.
12 Литература Математика. Алгебра. Функции. Анализ данных. 8 класс: Учебник для общеобразовательных учреждений / Г. В. Дорофеев и др. – М.: Дрофа, 2004 Гусев В. А., Мордкович А. Г. Математика: Справочные материалы: Книга для учащихся. – М.: Просвещение, 1988 Глейзер Г. И. История математики в школе. – М.: просвещение, 1982 Брадис В. М. Четырехзначные математические таблицы для среденй школы. М., просвещение, 1990 Окунев А. К. Квадратичные функции, уравнения и неравенства. Пособие для учителя. – М.: Просвещение, 1972 Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. М., Квант, 4/72. С.34. Дидактические материалы по алгебре. Математика (приложение к газете «Первое сентября»), 21/96, 10/97, 24/97, 40/2000. М. Я. Выгодский, Арифметика и алгебра в древнем мире, издательство «Наука» главная редакция физико-математической литературы, Москва 1967 К.А. Рыбников, История математики, издательство московского университета, Мурадова Р., Зенин Н.М., Математика г Энциклопедический словарь юного математика/ сост. А.П. Савин. – М.: Педагогика,1989 Алгебра: Учебник для 8 класса. Общеобразоват. Учреждений / А.Г.Мордкович, 2006 Садыхов С.Н., Попов В.В., Развитие творческой активности у учащихся в процессе решения заданий с использованием теоремы Виета. М.: НИИ школ, 1981 Бощенко О.В. «Математика» 5-9 классы
Приёмы устного решения квадратных уравнений. Квадратные уравнения – это фундамент, на котором стоит величественное здание алгебры. Квадратные уравнения. - презентация
Презентация на тему: " Приёмы устного решения квадратных уравнений. Квадратные уравнения – это фундамент, на котором стоит величественное здание алгебры. Квадратные уравнения." — Транскрипт:
1 Приёмы устного решения квадратных уравнений
2 Квадратные уравнения – это фундамент, на котором стоит величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, иррациональных уравнений и неравенств.Квадратные уравнения – это фундамент, на котором стоит величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, иррациональных уравнений и неравенств. В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения.В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.Однако имеются и другие приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.
3 Обобщить и систематизировать изученный материал по теме: «Квадратные уравнения». Научить учащихся приёмам устного решения квадратных уравнений. Развивать внимание и логическое мышление. Воспитывать культуру поведения.
4 b=oc=0b=0c0b0c=0 1 корень: x = 0 2корня: если : а и с имеют разные знаки Нет корней, если: а и с имеют одинаковые знаки2корня:
6 Теоремы Виета ЕслиОбратная Если
7 ЗАДАЧА Найти наиболее рациональным способом корни уравнения ответ
8 Приёмы устного решения квадратного уравнения приём «коэффициентов» приём «коэффициентов» приём «переброски» приём «переброски»
9 Приём «Коэффициентов»: 1) Если а+в+с=0, то 2) Если в = а + с, то Приём «Переброски» Можно решить уравнение х 2 + bx + ac = 0, И его корни разделить на а
11 Приёмы устного решения квадратных уравнений, то Например: Если Приём 1
12 Если b = a + c, то Приём 2 Ответ: х 1 = -1; х 2 = 13 Приём 3 Корни 9 и (-2). Делим числа 9 и ( -2) на 6: Ответ:
15 Другие приемы решения квадратных уравнений Если Например: Если Например: х 1 = 15; х 2 = 16 Например: если
17 1 вариант 2 вариант
18 Ответы 1 вариант2 вариант
19 Выводы: данные приёмы решения заслуживают внимания, поскольку они актуальны, но не отражены в школьных учебниках математики; овладение данными приёмами поможет учащимся экономить время и эффективно решать уравнения; потребность в быстром решении обусловлена применением тестовой системы вступительных экзаменов.
20 Когда уравненье решаешь дружок, Ты должен найти у него корешок. Значение буквы проверить несложно. Поставь в уравненье его осторожно. Коль верное равенство выйдет у вас, То корнем значенье зовите тотчас.
Фундамент, на котором покоится величественное здание алгебры
Квадратные уравнения-это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. В школьном курсе математики изучают формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений,которые позволяют очень быстро и рационально решать многие уравнения. Разберём некоторые из них.
Слайд 3 из презентации «Различные способы решения квадратных уравнений». Размер архива с презентацией 256 КБ.
Алгебра 8 класс
краткое содержание других презентаций«Свойства квадратного корня» - Самостоятельно. Вычислите. Решение упражнений. План урока. Вариант. Свойства квадратных корней. Литература. Ответы. Устная работа. Подведение итогов.
«Сокращённое умножение» - Проверочная работа. Задания на карточках. Проверка. Игра ''Смотри не ошибись.''. Формулы сокращенного умножения. Задания на отработку понимания математической речи на слух. Выбери правильный ответ. Игра Счастливый случай. Урок математики. Таблица.
«Решение биквадратных уравнений» - Решение задачи. Решение биквадратного уравнения. Цель урока. Веселые задачи. Пример. Решите уравнения. Классификация уравнений. Уравнения. Решение уравнений заменой. Устный счет. Квадратное уравнение.
«Рациональные уравнения» - Обсудите решение в четверках. Я математикой гармонию проверю. Рациональные уравнения. Уравнение. Самостоятельно закончите схему решения данного уравнения. 1 строчка – рациональное уравнение. Предложите свои варианты уравнений по схемам. При каких значениях переменной не имеет смысла выражение. Прочтите в книге определение рационального уравнения. Представить выражение в виде несократимой дроби. Представить в виде дроби выражение.
««Решение квадратных уравнений» 8 класс» - Уровень. Старушка. Черный вихрь. Представление. Решение квадратных уравнений по формуле. Театрализованный урок алгебры. Сколько корней имеет уравнение. Сказки. Клубок. Решите уравнение. Сказочник. Самостоятельная работа. Действующие лица. Баба-Яга. Задание. Крестьянский сын. Коэффициенты.
«Формула решения квадратных уравнений» - Аль-Хорезми. Примеры решения квадратных уравнений. Вывод формулы корней квадратного уравнения. Утверждения. Из истории решения квадратных уравнений. Уравнение не имеет корней. Установить верный ответ. Алгоритм решения квадратного уравнения. Теоретические сведения. Диофант Александрийский. Кроссворд. Квадратные уравнения. Задача из китайского трактата. Задания. Решение задачи при помощи языка программирования.
Читайте также:

