Рассчитать пусковой ток трансформатора
Обновлено: 26.07.2024
Рассчитать пусковой ток трансформатора
Сказал спасибо: 96
Пусковой ток трансформатора
Здравствуйте. Новенький однофазный трансформатор 380/220v 2500Вт без нагрузки в момент включения в четырех случаях из пяти "выбивает" автомат 16D. Совершенно ясно, что это зависит от угадывания момента перехода напряжения через ноль. Но от этого не легче. В устоявшемся режиме, под нагрузкой, ток через первичку 6А ( при этом транс еле-еле теплый). Даже 16ти амперный автомат не способен защитить трансформатор от длительной перегрузки током, скажем, 12А. Приходят в голову разные мысли, как это преодолеть. Например, можно поставить двухфазный автомат на 25А и, последовательно с ним, предохранители по 8А в цепь каждой фазы. Можно поставить устройство плавного пуска (дорогой, но безупречный вариант) Можно поставить твердотельное реле с управлением 220v и детектором перехода через ноль. Можно последовательно с первичкой поставить резистор. А как это решается вообще? Может я упускаю какой-нибудь крайне простой, веками известный способ? Как поступают другие?
Рассчитать пусковой ток трансформатора
При подключении трансформатора к сети (даже без нагрузки) ток через первичную обмотку трансформатора во время переходных процессов может достигать больших значений - во много раз превышающих ток в рабочем режиме полностью нагруженного трансформатора. Это явление хорошо известно и имеет простое объяснение; существует ряд более или менее успешных методов борьбы с ним. Тем не менее, для многих из тех, кто ранее имел дело только с трансформаторами крайне малой мощности (до нескольких десятков ватт), наличие очень больших пусковых токов в более мощных трансформаторах (несколько сотен ватт и более), становится неприятной неожиданностью.

Рис. %img:xmp1. Бросок тока при включении трансформатора
Пусковые токи наблюдаются и при включении маломощных трансформаторов, но там они столь невелики (ограничиваются большим активным сопротивлением первичной обмотки), что обычно их не принимают в расчёт. Например, на рис. %img:xmp1 изображён переходный процесс (начальный участок, первые пять периодов) для трансформатора мощностью порядка 50 Вт, включаемого без нагрузки. Здесь рассматривается самый неблагоприятный случай включения, когда оно происходит в момент прохождения напряжения источника через 0. График напряжения источника в условном масштабе размещён внизу (здесь амплитуда соответствует действующему напряжению 230 В).
ОглавлениеПусковой ток при включении трансформатора
Введение
Всем хорошо известна проблема зарядных токов, возникающих при подключении к источнику напряжения нагрузки со сглаживающими конденсаторами. А вот о том, что какие-то подобные неприятности могут возникнуть при включении в цепь индуктивности (например, первичной обмотки ненагруженного трансформатора в сеть переменного тока), многие даже не задумываются. Вероятно считается, что поскольку ток через индуктивность - неразрывная функция с точки зрения теории цепей, то если до подключения индуктивности ток через неё равен нулю, то и в момент сразу после подключения он будет таким же, нулевым. А потом, видимо, всё как-нибудь само собой уладится.
И на самом деле, в начальный момент ток через индуктивность равен нулю (если до момента включения он был нулевым). Но далее начинается переходный процесс, который при подключении индуктивности к источнику переменного напряжения имеет некоторые интересные особенности. Если рассматривается линейная индуктивность, то во время переходного процесса ток по абсолютной величине в определённые моменты времени может достигать значения, вдвое превышающего амплитуду тока в установившемся режиме (конкретное значение зависит от момента включения).
Если индуктивность имеет ферромагнитный сердечник, то её можно считать линейной только в грубом приближении и только пока ток достаточно мал, чтобы не происходило насыщение сердечника. Точнее говоря, мгновенные значения тока должны соответствовать какому-то линейному участку на кривой намагничивания материала сердечника; в случае обычного трансформатора в рабочем режиме используется участок, не заходящий значительно в область насыщения. Но во время переходного процесса, за счёт того, что мгновенные значения тока могут превышать максимальные (амплитудные) значения в установившемся режиме, насыщение становится возможным. Тем более что с точки зрения оптимального использования материалов, минимизации размеров, массы и стоимости устройства, амплитуду магнитной индукции в установившемся режиме выгодно выбирать как можно большей, вблизи насыщения.
В результате, в моменты во время переходного процесса после включения, когда происходит насыщение сердечника, магнитная проницаемость материала резко уменьшается, а значит, резко падают индуктивность и реактивное сопротивление. Ток возрастает, что приводит к ещё более глубокому насыщению сердечника. Таким образом, формируется импульс тока очень большой амплитуды. В наиболее неблагоприятных случаях он в десятки раз превышает амплитуду тока первичной обмотки полностью нагруженного трансформатора в установившемся режиме.
Причины появления пусковых токов
Для простоты будем рассматривать трансформатор, работающий в режиме холостого хода, т.е. без нагрузки. Такой трансформатор эквивалентен просто индуктивности, образованной первичной обмоткой трансформатора. Соответственно, переходные процессы при включении ненагруженного трансформатора будем исследовать как переходные процессы в индуктивности. На рис. %img:mdl изображена эквивалентная схема, соответствующая рассматриваемой задаче. Сопротивление R на схеме соответствует внутреннему активному сопротивлению обмотки трансформатора. В это сопротивление следует также включить сопротивление соединительных проводов и внутреннее сопротивление источника переменного напряжения, если они слишком велики, чтобы ими можно было пренебречь.

Рис. %img:mdl
Чтобы объяснить появление пусковых токов, необходимо учесть несколько важных моментов.
Прежде всего, будем иметь в виду то, что при создании трансформатора стараются добиться минимальных потерь. В частности, стремятся к тому, чтобы активное сопротивление обмоток было по возможности малым. В результате, как правило, обмотки являются высокодобротными индуктивностями - их реактивное сопротивление на рабочей частоте много больше (по крайней мере, в несколько раз больше) активного сопротивления: $$ \omega L \gg R, $$ где \(\omega\) есть циклическая частота источника, т.е. \( \omega = 2 \pi f \).
С другой стороны, конструируя трансформатор, стремятся к экономии материалов (для минимизации размеров, массы и стоимости трансформатора). Для минимизации размеров сердечника и обмоток выгодно, чтобы амплитуда магнитной индукции в сердечнике была по возможности большей, обычно при её выборе ориентируются на значение около 70%..80% от индукции насыщения (рис. %img:b_h).

Рис. %img:b_h
На рисунке жёлтым прямоугольником выделена область, содержащая участок кривой намагничивания, используемый в установившемся режиме работы трансформатора. Здесь предполагается, что сердечник выполнен из электротехнической стали марки 3414 (по ГОСТ 21427.1-83, при напряжённости магнитного поля 2500 А/м, магнитная индукция составляет не менее 1.88 Тл для этой стали). Петлю гистерезиса считаем достаточно узкой, чтобы в первом приближении наличием гистерезиса можно было пренебречь.
Наличие ферромагнитного сердечника делает нелинейной индуктивность, образованную обмоткой трансформатора. Но с другой стороны, при обычных для трансформатора уровнях амплитуды магнитной индукции, в грубом приближении, возможно использовать линейную модель.
Из теории электрических цепей мы знаем, что при подключении линейной индуктивности к источнику переменного напряжения, возникает переходный процесс, во время которого, при определённых условиях, пиковые значения тока через индуктивность могут вдвое превышать амплитуду тока в установившемся режиме (по крайней мере, это справедливо для высокодобротных индуктивностей). Конечно, пиковое значение, равное удвоенной амплитуде тока холостого хода - это совсем не те огромные броски тока, которые наблюдаются при включении трансформаторов в сеть. Но удвоенному значению тока соответствует удвоенное значение напряжённости магнитного поля, а этого более чем достаточно для вывода сердечника в область насыщения, с учётом того, что в установившемся режиме он и так работает с заходом в области, граничащие с областью насыщения.
Итак, с учётом сказанного, причина возникновения больших пусковых токов при включении трансформатора становится совершенно очевидной. Из соображений минимизации размеров и массы трансформатора, для его сердечника выбирают режим, при котором амплитуда магнитной индукции не намного меньше индукции насыщения. При подключении к источнику переменного напряжения, возникает переходный процесс, во время которого пиковый ток через индуктивность может вдвое превышать амплитуду тока в установившемся режиме, это справедливо для линейной индуктивности. Но в нашем случае рост тока приводит к выраженному проявлению нелинейных свойств индуктивности с ферромагнитным сердечником. Удвоение тока означает удвоение напряжённости магнитного поля, а значит, сердечник выходит в область насыщения. Магнитная проницаемость материала сердечника резко падает, соответственно очень сильно уменьшается реактивное сопротивление обмотки, ток через обмотку возрастает ещё больше. Как было указано, активное сопротивление обмотки мало по сравнению с индуктивным сопротивлением в нормальном режиме, поэтому при резком уменьшении реактивного сопротивления появляются импульсы тока с очень большими пиковыми значениями.
Следует отметить, что не каждое включение обязательно сопровождается одинаково большими пусковыми токами. Дело в том, что характер переходных процессов зависит от начальной фазы источника переменного напряжения (фазы в момент включения). Далее покажем, что наибольшие токи достигаются при подключении в момент, когда напряжение источника проходит через ноль. Если же подключить трансформатор (индуктивность) в момент, когда напряжение источника достигает амплитудного значения, переходный процесс отсутствует вовсе, сразу начинается работа в установившемся режиме. Соответственно, при подключении в некоторые промежуточные моменты между указанными крайними вариантами, будет наблюдаться более или менее выраженный переходный процесс, и в случае насыщения сердечника - появляться большие или меньшие пусковые токи. Таким образом, если производить включение трансформатора в произвольные, случайные моменты времени, то некоторые включения могут происходить вполне "спокойно", если в этот момент мгновенное напряжение источника по абсолютной величине находится вблизи амплитудного значения.
Более детальный анализ показывает, что присутствие нагрузки, по крайней мере, чисто активной, не изменяет принципиально характер переходных процессов. Наблюдаются небольшие количественные изменения: переходный процесс оказывается менее продолжительным, пиковые значения тока несколько ниже. Что можно объяснить внесением дополнительного эквивалентного сопротивления в цепь первичной обмотки при наличии нагрузки. Что касается установившегося режима, то, как известно, амплитуда магнитной индукции в сердечнике трансформатора практически не зависит от нагрузки и примерно равна амплитуде магнитной индукции на холостом ходу. А потому, если в установившемся режиме на холостом ходу нет насыщения сердечника, то оно не будет происходить и в нагруженном трансформаторе.
Способы борьбы с пусковыми токами
Зачастую наличие пускового тока допустимо и специальных мер по борьбе с ним не требуется. Но если он оказывается слишком велик, нетрудно найти способы его ограничения. С учётом причин данного явления, можно предложить следующие варианты: изменение конструкции трансформатора таким образом, чтобы переходный процесс при включении не приводил к насыщению сердечника; выбор благоприятного момента включения; первоначальное включение через ограничивающий ток резистор с последующим замыканием этого резистора.
1. При проектировании трансформатора можно примерно в 1.5..2 раза снизить амплитудное значение магнитной индукции в сердечнике (в установившемся режиме) относительно традиционно принятых значений. Тогда во время переходного процесса, насыщения сердечника не происходит и проблема пусковых токов полностью устраняется. На практике это достигается соответствующим увеличением числа витков для сердечника данного сечения.
В самом деле, если считать, что амплитуда напряжённости магнитного поля в сердечнике на холостом ходу $$ H = \frac l, $$ то амплитуда магнитной индукции $$ B = <\mu>_0 \mu H = \frac <<\mu>_0 \mu n I> l, $$ где \(<\mu>_0\) - магнитная постоянная; \( \mu\ \) - магнитная проницаемость материала сердечника; n - количество витков; I - амплитуда тока в обмотке; l - средняя длина магнитной линии в магнитопроводе (или длина магнитопровода, с целью грубой оценки можно пренебречь тем, что линии, проходящие через разные точки сечения магнитопровода, имеют разную длину). Амплитуду тока холостого хода можно выразить через реактивное сопротивление индуктивности обмотки и амплитуду напряжения источника, к которому подключена индуктивность (активным сопротивлением пренебрегаем, считая индуктивность высокодобротной): $$ I \approx \frac U , $$ индуктивность L примем равной $$ L = \frac <<\mu>_0 \mu n^2 S> l $$ (S - площадь поперечного сечения магнитопровода). Тогда окончательно получаем $$ B = \frac <<\mu>_0 \mu n> l \frac _0 \mu n^2 S> = \frac U $$ или $$ n=\frac U , $$ т.е., действительно, меньшему значению амплитуды B при прочих равных условиях соответствует большее количество витков n.
Однако предложенный способ устранения пусковых токов довольно затратен. Увеличение количества витков в обмотках означает увеличение длины провода, а значит объёма и массы обмотки. Кроме того, чтобы потери в обмотке трансформатора не увеличились при увеличении длины провода, необходимо соответственно увеличить сечение провода, т.е. размеры обмотки увеличиваются ещё в большей степени. В результате такая обмотка не поместится в окно исходного магнитопровода, значит, потребуется выбрать магнитопровод большего размера.
Трансформатор, полностью свободный от пусковых токов получается больше, тяжелее и дороже, чем обычный трансформатор такой же мощности.
2. Можно усложнить схему включения так, чтобы подключение трансформатора к сети происходило в наиболее выгодный момент - в момент, когда мгновенное напряжение в сети достигает амплитудного значения. Потребуется электронный ключ достаточной мощности (например, симистор) для быстрой коммутации трансформатора и схема управления. Задача усложняется тем, что напряжение в сети может быть сильно зашумлено, а кроме того, схема должна отрабатывать не только первоначальное включение, но и возможные кратковременные перебои в электроснабжении.
Развивая этот подход, путём совершенствования схемы управления и используя метод фазовой регулировки напряжения с помощью симистора, придём к системе ограничения тока независимо от причины его повышения сверх заданных пределов (пуск, перегрузка, короткое замыкание).
3. Можно ограничить пусковой ток за счёт токоограничивающего резистора, который через некоторое время после включения трансформатора замыкается накоротко. Здесь уже не требуется использование быстродействующих ключей (применимы медленные релейные схемы) и в целом схема включения получается проще. Возможные проблемы - как и в предыдущем случае, переходный процесс возникает не только при первоначальном включении, но и при восстановлении напряжения в сети после временных перебоев питания. Кроме того, пусковой ток не отсутствует полностью, но он ограничен определённым значением.

Рис. %img:ntc
В простейшем случае ток может быть ограничен подходящим NTC термистором (рис. %img:ntc). Но при повторных включениях, после отключения до последующего включения должно выдерживаться время в несколько десятков секунд, иначе термистор не успеет охладиться, его сопротивление будет оставаться низким и функцию ограничения тока он выполнять не будет.
4. Не требуется специальных мер для ограничения пускового тока, если его наибольшее значение допустимо как для сети, так и для трансформатора. При этом, если трансформатор достаточно мощный, может потребоваться использование более инерционных защитных автоматических выключателей (класса C) в цепи питания трансформатора, которые не успевают срабатывать за время переходного процесса.
Не требуется ограничивать пусковой ток маломощных трансформаторов - активное сопротивление их первичной обмотки столь велико (от десятков Ом до нескольких тысяч Ом у самых маломощных), что оно естественным образом ограничивает пусковой ток.
Переходные процессы при подключении индуктивности к источнику переменного напряжения
Поскольку этот вопрос тесно связан с проблемой пусковых токов, рассмотрим подробнее переходные процессы при подключении линейной индуктивности к источнику переменного напряжения. Будем анализировать переходный процесс в RL-цепи, образованной индуктивностью катушки L и её активным сопротивлением R (внутреннее сопротивление источника переменного напряжения и сопротивление соединительных проводов считаем малыми и пренебрегаем этими сопротивлениями, либо включаем их в состав R).

Рис. %img:ml
Если u - мгновенное напряжение источника, то рассматриваемая электрическая цепь описывается уравнением $$ \begin u = iR + L \frac , \label \end $$ которое является линейным дифференциальным уравнением относительно i.
Из теории дифференциальных уравнений нам известно, что общее решение линейного уравнения представляет собой сумму общего решения соответствующего ему однородного уравнения и частного решения исходного уравнения. Или, в терминологии теории цепей, интересующая нас реакция цепи на внешнее воздействие равна сумме свободной и вынужденной (установившейся) составляющей, т.е. $$ i = i_1 + i_2, $$ где i1 - общее решение однородного уравнения (которое получается из исходного (\ref), если положить u = 0), $$ \begin i_1 R + L \frac = 0, \label \end $$ i2 - частное решение исходного уравнения (\ref).
Свободная составляющая i1 находится элементарно: $$ i_1 R + L \frac = 0, \\ \frac = - \frac R L i_1, \\ \frac = - \frac R L dt, \\ i_1 = A e^, $$ где A - постоянная, определяемая начальными условиями.
Вынужденную составляющую i2 также не составляет труда найти. Допустим, мгновенное напряжение источника $$ \begin u = U \sin(\omega t + \phi), \label \end $$ где U - амплитуда источника; \( \omega \) - циклическая частота, \( \omega = 2 \pi f \); \(\phi\) - начальная фаза, т.е. величина, определяющая мгновенное значение напряжения источника в начальный момент времени (за начальный принимаем момент подключения индуктивности к источнику).
Как известно, при не слишком жёстких требованиях к свойствам цепи (которые здесь выполняются), установившаяся реакция (в данном случае - ток i2) на синусоидальное воздействие, также является синусоидальной, причём имеет ту же частоту. И может быть легко найдена, например, с помощью метода комплексных амплитуд.
Или можно поступить иначе. Подставим в уравнение в качестве искомой синусоидальную функцию с неизвестной амплитудой и фазой. То есть, вынужденную составляющую тока (установившуюся реакцию на внешнее воздействие) будем искать в виде $$ \begin i_2 = I \sin(\omega t + \alpha), \label \end $$ здесь I, \( \alpha \) - пока ещё неизвестные амплитуда и начальная фаза искомого решения. Для того чтобы найти эти величины, подставим выражение для i2 в качестве i в уравнение (\ref). С учётом (\ref) получим $$ \begin U \sin(\omega t + \phi) = IR \sin(\omega t + \alpha) + I \omega L \cos(\omega t + \alpha). \label \end $$
Как известно, выражение вида $$ a \sin x + b \cos x, $$ где a, b - произвольные постоянные, всегда можно преобразовать следующим образом: $$ a \sin x + b \cos x = \sqrt \sin(x + \psi), $$ где \(\psi\) определяется из условий $$ \cos \psi = a / \sqrt, \\ \sin \psi = b / \sqrt, $$ а если одновременно a = 0 , b = 0 , то \(\psi\) - любое число. Обосновать это преобразование чрезвычайно просто, подробнее об этом можно посмотреть в статье "Тригонометрические функции и формулы".
Применяя данное преобразование для правой части уравнения (\ref), получаем уравнение вида $$ \begin U \sin(\omega t + \phi) = I \sqrt^2 L^2> \sin(\omega t + \alpha + \beta), \label \end $$ где $$ \begin \cos \beta = \frac R <\sqrt^2 L^2>>, \\ \sin \beta = \frac <\omega L><\sqrt^2 L^2>>. \label \end $$ Равенство (\ref) должно выполняться в любой момент времени t, что возможно, если только одновременно выполняются два условия: $$ \begin U = I \sqrt^2 L^2>, \\ \phi = \alpha + \beta \end $$ что можно также записать как $$ I = \frac U <\sqrt^2 L^2>>, \\ \alpha = \phi - \beta. $$ Величина \(\beta\) определяется из равенств (\ref) и представляет собой отставание по фазе тока от напряжения в рассматриваемой RL цепи. Как видим из (\ref), это отставание находится в пределах 0..\(\pi/2\). Если катушка индуктивности высокодобротная, т.е. $$ \omega L \gg R, $$ то отставание тока по фазе близко (чуть меньше) к четверти периода: $$ \beta \approx \pi/2. $$
Итак, возвращаясь к искомой функции (\ref), запишем $$ i_2 = I \sin(\omega t + \phi - \beta) $$ или $$ i_2 \approx I \sin(\omega t + \phi - \pi/2) $$ для высокодобротной катушки. И в том, и в другом случае под I подразумевается амплитуда тока через индуктивность в установившемся режиме, т.е. $$ I = \frac U ^2 L^2>> $$
Далее будем рассматривать только интересующий нас сейчас случай высокодобротной катушки, а значит $$ i_2 \approx I \sin(\omega t + \phi - \pi/2) $$ или $$ i_2 \approx - I \cos(\omega t + \phi). $$ Итак, мы нашли свободную и вынужденную составляющие реакции (тока в цепи) на воздействие (синусоидальное напряжение источника), а значит, можем записать общее решение для тока через индуктивность: $$ i = i_1 + i_2 \approx A e^ - I \cos(\omega t + \phi). $$ Постоянную A найдём из начальных условий. Если сделать вполне естественное предположение о том, что до подключения индуктивности к источнику ток в индуктивности отсутствовал, то можем записать $$ i(0) = 0, \\ A - I \cos \phi \approx 0, \\ A \approx I \cos \phi. $$
Тогда окончательно получаем, что ток в катушке $$ i \approx (I \cos \phi) e^ - I \cos(\omega t + \phi). $$ То есть, имеем переменную, синусоидальную составляющую тока с амплитудой I (ток в катушке в установившемся режиме) и затухающую по экспоненте составляющую с наибольшим по модулю значением \( |I \cos \phi| \).
Можно показать, что для катушки с высокой добротностью, в течение нескольких первых периодов колебаний источника, выполняется условие $$ e^ \approx 1, $$ а значит для некоторого промежутка времени, непосредственно следующего за моментом подключения индуктивности к источнику, выполняется соотношение $$ i \approx I \cos \phi - I \cos(\omega t + \phi). $$ Тогда пиковое (наибольшее по абсолютной величине) значение тока i, составляет $$ |i|_ \approx I |\cos \phi| + I = I (|\cos \phi| + 1). $$ Как видим, оно зависит от начальной фазы источника переменного напряжения. Может достигать 2 I, т.е. двойного значения амплитуды в установившемся режиме (рис. %img:t0), при условии, что \( \phi = 0 \) или \( \phi = \pi \). Иначе говоря, если в момент подключения индуктивности, мгновенное напряжение источника проходит через 0.

Рис. %img:t0
Если же подключение происходит в момент достижения напряжением источника амплитудного значения, переходный процесс отсутствует, и цепь сразу начинает работать в установившемся режиме (рис. %img:t2). Очевидно, что в таком случае пиковое значение тока равно просто амплитуде тока в установившемся режиме.

Рис. %img:t2
Наконец, если в момент подключения индуктивности, мгновенное напряжение источника не равно нулю, но и не достигло амплитудного значения, то будет наблюдаться переходный процесс, во время которого пиковое значение тока будет больше I, но меньше 2I, где I - амплитуда тока в установившемся режиме (рис. %img:t3).

Рис. %img:t3
На рисунках %img:t0, %img:t2, %img:t3 внизу в условном масштабе изображены графики напряжения источника, которые помогают проследить влияние начальной фазы напряжения на протекание переходного процесса в цепи.
Ссылки *
* Если ссылка не работает, не забывайте о существовании веб-архива и поисковых систем.
Что такое пусковой ток двигателя?
Что такое пусковой ток, как его посчитать, увидеть и измерить?
Решил разобраться в теме, про которую написано предостаточно, но суть неясна. Вопрос касается пуска электродвигателей, при котором возникает так называемый пусковой ток.
Пусковой ток и его кратность
Номинальный ток всегда указан на шильдике двигателя:

Номинальный ток двигателя для разных напряжений и схем включения
Кратность пускового тока . На шильдике его обычно нет, а в документации и на сайтах производителей он присутствует:
Параметры двигателей. Кратность пускового тока
Судя по каталогам (их можно будет скачать в конце статьи, как обычно у меня), пусковой ток превышает номинальный в пределах от 3,5 до 8,5 раз.На самом деле не так всё просто, начинаем копать глубже.
Как узнать пусковой ток?
Кратность пускового тока (отношение пускового тока к номинальному) найти в документации на двигатель бывает не так-то просто. Но его можно измерить (оценить, узнать) самому. Вот навскидку несколько способов:

Какой вред от пускового тока?
Как уменьшить пусковой ток асинхронного двигателя
Решить проблему большого пускового тока электрически можно двумя путями:
В современном оборудовании двигатели мощнее 2,2 кВт практически никогда напрямую не включают, поэтому для них пусковые токи рояли не играют. Для уменьшения пускового тока (и не только) в основном применяют преобразователи частоты, о которых будут отдельные статьи.
Как снизить вред от пускового тока?
Но напоминаю, что мы тут занимаемся не устранением последствий, а предотвращением проблем, поэтому погнали дальше.
Время действия и величина пускового тока
Длительностью пускового тока будем считать время, в течение которого ток понижается от максимума (Iп) до номинала (Iн). Эта длительность фактически равна времени разгона от нуля до номинальной скорости вращения.
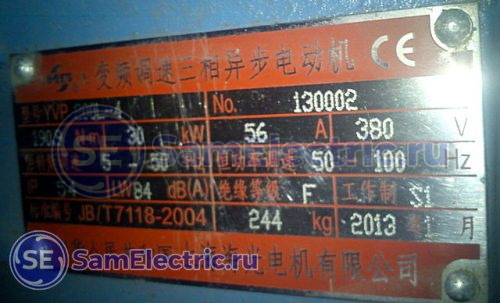
Шильдик китайского электродвигателя 30 кВт
Тепловое действие пускового тока
Если перейти к формулам, пусковой ток оказывает тепловое действие на электродвигатель, которое описывается так называемым интегралом Джоуля. Если по простому, то тепловая энергия, производимая электрическим током, пропорциональна квадрату тока, умноженному на время. Обозначается эта величина через I2t.
Хорошая новость в том, что защитный автомат имеет примерно такую же тепловую (время-токовую) характеристику, что и время-токовая характеристика разгона двигателя.

Время-токовые характеристики защитного автомата
Что видим? Для защиты двигателя используются в основном автоматы с характеристикой D, как раз для того, чтобы меньше реагировать на кратковременные перегрузки. Подробнее здесь.
А для пускового тока двигателя график будет примерно такой:
График пускового тока (теоретический) при Кп = 6
Понятно, что из-за потерь время разгона будет больше, оно обозначено на графике через tп`.
Теперь повернём последний график, чтобы привести оси к одной системе координат:
Время от тока, если можно так выразиться
Не правда ли, весьма похоже на время-токовую характеристику защитного мотор-автомата?
Реальные измерения тока
Я использовать вот такой шунт:

Шунт для измерения пускового тока при помощи осциллографа

Мотор-редуктор, на котором измеряем пусковой ток
Шнек на момент пуска был полным, поэтому его рабочий ток (7,7 А, измерено клещами) был почти равен номинальному (8,9 А, видно на шильдике).

Шильдик двигателя вертикального шнека
Ситуация по пусковому току видна на осциллографе:
Осциллограмма пускового тока 500 мс/дел
Приблизим интересующий момент, ускорив развертку до 100 мс/дел:
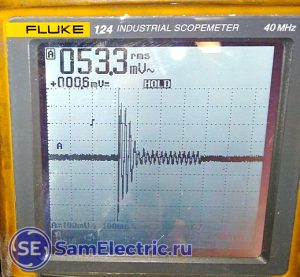
Осциллограмма пускового тока 100 мс/дел
Тут уже легко увидеть синус питающего тока и оценить коэффициент кратности пускового тока Кп, который примерно равен 4.
Ещё приблизим момент истины (до 50 мс/дел):
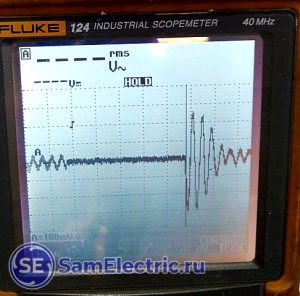
Тут уже видны хорошо и переходные процессы, обусловленные индуктивностью и ЭДС самоиндукции обмоток двигателя. Этот импульс, длительность которого гораздо меньше периода сети 20 мс, даёт хорошую помеху с широким спектром в питающую сеть и радиоэфир.
Ещё один повод для использования ПЧ? Не совсем, там с помехами ситуация гораздо хуже!
• В.Л.Лихачев. Асинхронные электродвигатели. 2002 г. / Книга представляет собой справочник, в котором подробно описано устройство, принцип работы и характеристики асинхронных электродвигателей. Приводятся справочные данные на двигатели прошлых лет выпуска и современные. Описываются электронные пусковые устройства (инверторы), электроприводы., djvu, 3.73 MB, скачан: 6418 раз./
• Беспалов, Котеленец - Электрические машины / Рассмотрены трансформаторы и электрические машины, используемые в современной технике. Показана их решающая роль в генерации, распределении, преобразовании и утилизации электрической энергии. Даны основы теории, характеристики, режимы работы, примеры конструкций и применения электрических генераторов, трансформаторов и двигателей., pdf, 16.82 MB, скачан: 1997 раз./
• М.М. Кацман - Электрические машины / Некоторые говорят, что это лучший учебник по электротехнике. В книге рассматриваются теория, принцип действия, устройство и анализ режимов работы электрических машин и трансформаторов как общего, так и специального назначения, получивших распространение в различных отраслях техники., pdf, 22.12 MB, скачан: 1673 раз./
• Каталог двигателей Электромаш / Асинхронные электродвигатели с короткозамкнутым ротором - каталог производителя, pdf, 3.13 MB, скачан: 1169 раз./
• Каталог двигателей ВЭМЗ / Параметры и каталог двигателей, pdf, 3.53 MB, скачан: 994 раз./
• Дьяков В.И. Типовые расчеты по электрооборудованию / Практические расчеты по электрооборудованию, теоретические сведения, методики расчета, примеры и справочные данные., zip, 1.53 MB, скачан: 2027 раз./
• Карпов Ф.Ф. Как проверить возможность подключения нескольких двигателей к электрической сети / В брошюре приведен расчет электрической сети на колебание напряжения при пуске и самозапуске асинхронных двигателей с короткозамкнутым ротором и синхронных двигателей с асинхронным пуском. Рассмотрены условия, при которых допустим пуск и самозапуск двигателей. Изложение методов расчета иллюстрируется числовыми примерами. Брошюра предназначена для квалифицированных электромонтеров в качестве пособия при выборе типа электродвигателей, присоединяемых к коммунальной или промышленной электросети., zip, 1.9 MB, скачан: 1229 раз./
• Руководство по эксплуатации асинхронных двигателей / Настоящее руководство содержит наиболее важные указания по транспортировке, приемке, хранению, монтажу, пусконаладке, эксплуатации, техническому обслуживанию, поиску неисправностей и их устранению для электродвигателей производства «Электромашина». Руководство по эксплуатации предназначено для трехфазных асинхронных электродвигателей низкого и высокого напряжений серий А, АИР, МТН, МТКН, 4МТМ, 4МТКМ, ДА304, А4., pdf, 7.54 MB, скачан: 2247 раз./
• Каталог двигателей АИР / Каталог двигателей АИР - мощность от 0,12 до 315 кВт; частота вращения 3000, 1500, 1000, 750 об/мин; напряжение сети 220/380 В, 380/660 В;, pdf, 1.07 MB, скачан: 856 раз./
• Ломоносов, В.Ю.; Поливанов, К.М.; Михайлов, О.П. Электротехника. / Ломоносов, В.Ю.; Поливанов, К.М.; Михайлов, О.П. Электротехника. Одна из лучших книг, посвящённых основам электротехники. Изложение начинается с самых основ: объясняется, что такое напряжение, сила тока и сопротивление, приводятся указания по расчёту простейших электрических цепей, рассказывается о взаимосвязи и взаимозависимости электрических и магнитных явлений. Объясняется, что такое переменный ток, как устроен генератор переменного тока. Описывается, что такое конденсатор и что собой представляет катушка индуктивности, какова их роль в цепях переменного тока. Объясняется, что такое трёхфазный ток, как устроены генераторы трёхфазного тока и как организуется его передача. Отдельная глава посвящена полупроводниковым приборам: в ней речь идёт о полупроводниковых диодах, о транзисторах и о тиристорах; об использовании полупроводниковых приборов для выпрямления переменного тока и в качестве полупроводниковых ключей. Коротко описываются достижения микроэлектроники. Последняя треть книги целиком посвящена электрическим машинам, агрегатам и оборудованию: в 10 главе речь идёт о машинах постоянного тока (генераторах и двигателях); 11 глава посвящена трансформаторам; о машинах переменного тока (однофазных и трёхфазных, синхронных и асинхронных) подробно рассказывается в 12 главе; выключатели, электромагниты и реле описываются в главе 13; в главе 14 речь идёт о составлении электрических схем. Последняя, 15 глава, посвящена измерениям в электротехнике. Эта книга - отличный способ изучить основы электротехники, понять основополагающие принципы работы электрических машин и агрегатов., zip, 13.87 MB, скачан: 1998 раз./
Ещё пособие по двигателям:
• Пуск и защита двигателей переменного тока / Пуск и защита двигателей переменного тока. Системы пуска и торможения двигателей переменного тока. Устройства защиты и анализ неисправностей двигателей переменного тока. Руководство по выбору устройств защиты. Руководство от Schneider Electric, pdf, 1.17 MB, скачан: 1588 раз./
Читайте также:

