Обрыв фазы в трехфазной цепи со схемой соединения звезда с нулевым проводом
Обновлено: 26.07.2024
Аварийные режимы трёхфазной цепи при соединении нагрузки в «звезду»
Аварийными являются режимы, возникают при коротких замыканиях в нагрузке или в линиях и обрыве проводов. Остановимся на некоторых типичных аварийных режимах.
Обрыв нейтрального провода при несимметричной нагрузке
В симметричном режиме IN = 0, поэтому обрыв нейтрального провода не приводит к изменению токов и напряжений в цепи и такой режим не является аварийным. Однако, при несимметричной нагрузке IN ≠ 0, поэтому обрыв нейтрали приводит к изменению всех фазных токов и напряжений. На векторной диаграмме напряжений точка «0» нагрузки, совпадающая до этого с точкой «N» генератора, смещается таким образом, чтобы сумма фазных токов оказалась равной нулю (рис.3.9). Напряжения на отдельных фазах могут существенно превысить номинальное напряжение.
Обрыв фазы при симметричной нагрузке в схеме с нулевым проводом
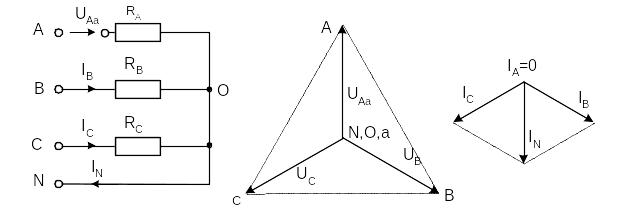
При обрыве провода, например, в фазе А ток этой фазы становится равным нулю, напряжения и токи в фазах В и С не изменяются, а в нулевом проводе появляется ток IN = IB + IC. Он равен току, который до обрыва протекал в фазе А (рис. 3.10).
Обрыв фазы при симметричной нагрузке в схеме без нулевого провода
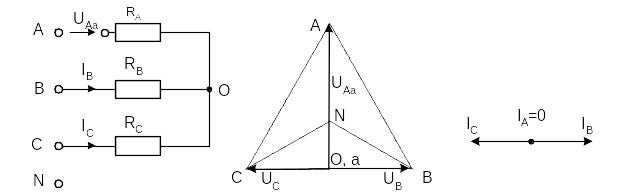
При обрыве, например, фазы А сопротивления RA и RB оказываются соединёнными последовательно и к ним приложено линейное напряжение UBC. Напряжение на каждом из сопротивлений составляет от фазного напряжения в нормальном режиме. Нулевая точка нагрузки на векторной диаграмме напряжений смещается на линию ВС и при RB = RC находится точно в середине отрезка ВС (рис.3.11)
Короткие замыкания
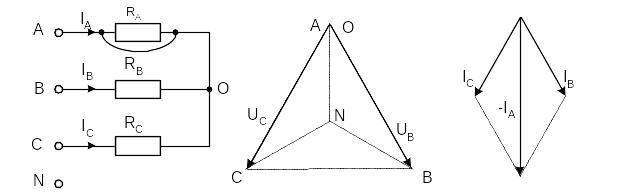
При коротком замыкании фазы нагрузки в схеме с нулевым проводом ток в этой фазе становится очень большим (теоретически бесконечно большим) и это приводит к аварийному отключению нагрузки защитой. В схеме без нулевого провода при замыкании, например, фазы А, нулевая точка нагрузки смещается в точку «А» генератора. Тогда к сопротивлениям фаз В и С прикладываются линейные напряжения. Токи в этих фазах возрастают в раз, а ток в фазе А – в 3 раза (рис. 3.12).
Короткие замыкания между линейными проводами и в той и в другой схеме приводят к аварийному отключению нагрузки.
Аварийные режимы трёхфазной цепи при соединении нагрузки в «треугольник»
При коротких замыканиях в фазах нагрузки или между линейными проводами токи резко возрастают и происходит аварийное отключение установки защитой.
Обрывы фаз или линейных проводов при соединении нагрузки в треугольник не приводят к перегрузкам по токам или напряжениям, как это иногда случается при соединении нагрузки в звезду.
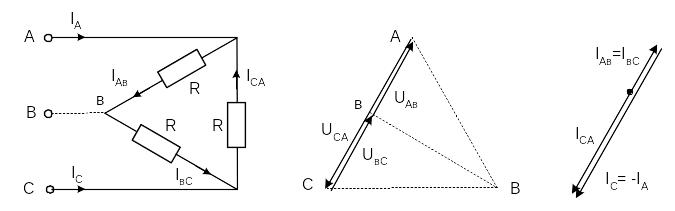
При обрыве одной фазы нагрузки (рис. 3.13) ток этой фазы становится равным нулю, а в оставшихся двух фазах ток не меняется. Два линейных тока уменьшаются в раз, т. е. становятся равными фазному току, а третий остаётся неизменным.

При обрыве линейного провода (например, В) фазные сопротивления RAB и RBC оказываются соединёнными последовательно и включёнными параллельно с сопротивлением RCA на напряжение UCA (рис. 3.14). Цепь фактически становится однофазной.
При одновременном обрыве линейного провода и одной фазы нагрузки цепь также становится однофазной (рис. 3.15 и 3.16).
§60. Схема соединения «звездой»
При соединении фазных обмоток источника трехфазного тока (например, генератора) по схеме «звезда с нулевым проводом» концы его трех обмоток соединяют в общий узел 0, который называется нулевой точкой, или нейтралью источника (рис. 206).

Рис. 206. Схема «звезда с нулевым проводом», направление в ней линейных и фазных токов и напряжений
Приемники электрической энергии объединяют в три группы ZA, ZB и Zc (фазы нагрузки), концы которых также соединяют в общий узел 0′ (нулевая точка, или нейтраль нагрузки). Обмотки источника соединяют с фазами нагрузки четырьмя проводами. Провода 1, 2 и 3, присоединенные к началам фазных обмоток (А, В, С), называют линейными. Провод 4, соединяющий нулевые точки 0 и 0′, называют нулевым, или нейтральным.
Напряжения uА, uв и uс между началами и концами обмоток отдельных фаз источника или фаз нагрузки ZA, ZB и Zc называют фазными. Они равны также напряжениям между каждым из линейных проводов и нулевым проводом. При отсутствии потери напряжения в обмотках источника (при холостом ходе) фазные напряжения равны соответствующим э. д. с. в этих обмотках.
Фазными токами iA, iB, ic называют токи, протекающие по обмоткам источника или фазам нагрузки ZA, ZB и Zc. Напряжения uAB, uBC, uCA между линейными проводами и токи, проходящие по этим проводам, называют линейными.
Примем условно за положительное направление токов iA, iB и ic в фазах источника — от конца соответствующей фазы к ее началу,в фазах нагрузки — от начала к концу, а в линейных проводах — от источника к приемнику.
Будем считать положительными напряжения uА, uB и uC в фазах источника и нагрузки, если они направлены от начала фаз к концам, а линейные напряжения uАВ, uBC, uСА — если они направлены от предыдущей фазы к последующей.
Из рис. 206 следует, что в схеме «звезда» линейные токи равны фазным, т. е. Iл = Iф, так как при переходе от фазы источника или нагрузки к линейному проводу нет каких-либо ответвлений.
Мгновенные значения напряжений согласно второму закону Кирхгофа:
Переходя от мгновенных значений напряжений к их векторам, имеем:
Следовательно, линейное напряжение равно разности векторов соответствующих фазных напряжений.
По полученным векторным уравнениям можно построить векторную диаграмму (рис. 207, а), которую можно преобразовать в диаграмму (рис. 207,б). Из этой диаграммы видно, что в симметричной трехфазной системе векторы линейных напряжений →uAB, →uВС, →uСА образуют равносторонний треугольник ABC, внутри которого расположена симметричная трехлучевая звезда фазных напряжений →uА, →uВ, →uС.
В равнобедренных треугольниках АОВ, ВОС и СОА основание равно Uл две другие стороны — Uф и острый угол между этими сторонами и основанием составляет 30°.

Рис. 207. Векторные диаграммы напряжений для схемы «звезда с нулевым проводом»
Таким образом, в трехфазной системе, соединенной по схеме «звезда с нулевым проводом», линейное напряжение больше фазного в √З раз. Величина √З = 1,73 положена в основу шкалы номинальных напряжений переменного тока: 127, 220, 380 и 660 В. В этом ряду каждое следующее значение напряжения больше предыдущего в 1,73 раза.
В нулевом проводе проходит ток i0, мгновенное значение которого равно алгебраической сумме мгновенных значений токов, проходящих в отдельных фазах: i0 = iA+iB+iC.
Переходя от мгновенных значений токов к их векторам, имеем:
Векторы токов →iА, →iВ и →iС сдвинуты относительно векторов соответствующих напряжений →uA, →uB, →uС на углы →iA, →iB, →iC (рис. 208, а). Значения этих углов зависят от соотношения между активным и реактивным сопротивлениями, включенными в данную фазу.
На этой же диаграмме показано сложение векторов →iА, →iВ и →iC для определения вектора тока →i0. Обычно ток →i0 меньше токов

Рис. 208. Векторные диаграммы напряжений и токов в отдельных фазах для схемы «звезда с нулевым проводом» при неравномерной (а) и равномерной (б) нагрузках фаз
IA, 1В и IC в линейных проводах, поэтому нулевой провод имеет площадь поперечного сечения, равную или даже несколько меньшую площади сечения линейных проводов.
В схеме «звезда с нулевым проводом» приемники электрической энергии можно включать на два напряжения: линейное Uл (при подключении к двум линейным проводам) и фазное UФ (при подключении к нулевому и одному из линейных проводов).
Схема «звезда без нулевого провода».
При равномерной или симметричной нагрузке всех трех фаз, когда во всех фазах включены одинаковые активные и реактивные сопротивления (RA =RB = RC и ХA=ХВ=ХС), фазные токи iA, iB и iC будут равны по величине и сдвинуты от соответствующих фазных напряжений на равные углы. В этом случае получаем симметричную систему токов, при которой токи iA, iB, iC будут сдвинуты по фазе друг относительно друга на угол 120°, а ток i0 в нулевом проводе в любой момент времени равен нулю (рис. 208,б).
Очевидно, что при равномерной нагрузке можно удалить нулевой провод и передавать электрическую энергию источника к приемнику по трем линейным проводам 1, 2 и 3 (рис. 209).

Рис. 209. Схема «звезда без нулевого провода»
Такая схема называется «звезда без нулевого провода». При трехпроводной системе передачи электрической энергии в каждое мгновение ток по одному (или двум) проводу проходит от источника трехфазного тока к приемнику, а по двум другим (или одному) протекает обратно от приемника к источнику (рис. 210).

Рис 210. Кривые изменения токов в линейных проводах (а) при трехпроводной системе и направление в них токов в различные моменты времени (б в, г)
Векторная диаграмма напряжений для схемы «звезда без нулевого провода» при равномерной нагрузке фаз будет такая же, как и для схемы «звезда с нулевым проводом» (см. рис. 207).
Такими же будут и соотношения между фазными и линейными токами и напряжениями:
Следует отметить, что схема «звезда без нулевого провода» может быть применена только при равномерной нагрузке фаз. Практически это имеет место лишь при подключении к источникам трехфазного тока электрических двигателей, так как каждый трехфазный электродвигатель снабжен тремя одинаковыми обмотками, которые равномерно нагружают все три фазы.
При неравномерной нагрузке напряжения на отдельных фазах нагрузки будут различными. На некоторых фазах (с меньшим сопротивлением) напряжение уменьшится, а на других увеличится по сравнению с нормальным, что является недопустимым.
Практически неравномерная нагрузка фаз возникает при питании трехфазным током электрических ламп, так как в этом случае распределение тока между всеми тремя фазами не может быть гарантировано (отдельные лампы могут включаться и выключаться в индивидуальном порядке). Особенно опасны в схеме «звезда без нулевого провода» обрыв или короткое замыкание в одной из фаз.
Можно показать путем построения соответствующих векторных диаграмм, что при обрыве в одной из фаз напряжение в других двух фазах уменьшается до половины линейного, вследствие чего лампы, включенные в эти фазы, будут гореть с недокалом.
При коротком замыкании в одной из фаз напряжение в других фазах увеличивается до линейного, т. е. в √З раз, и все лампы, включенные в этих фазах, перегорят. Поэтому при схеме «звезда с нулевым проводом» во избежание разрыва цепи нулевого провода в ней не устанавливают предохранители и выключатели.
Цепи при соединении нагрузки в треугольник
Аварийный режим при соединении звездой с нейтральным проводом в случае обрыва нейтрали и одной из фаз. Схема аварийного случая. Векторные диаграммы токов и напряжений для такого случая. Последствия аварийного случая.
Аварийными являются режимы, возникают при коротких замыканиях в нагрузке
или в линиях и обрыве проводов. Остановимся на некоторых типичных аварийных
Обрыв нейтрального провода при несимметричной нагрузке
В симметричном режиме IN= 0, поэтому обрыв нейтрального провода не приводит
к изменению токов и напряжений в цепи и такой режим не является аварийным. Однако,
при несимметричной нагрузке IN¹ 0, поэтому обрыв нейтрали приводит к изменению всех
фазных токов и напряжений. На векторной диаграмме напряжений точка «0» нагрузки,
совпадающая до этого с точкой «N» генератора, смещается таким образом, чтобы сумма
фазных токов оказалась равной нулю (рис.8.4.1). Напряжения на отдельных фазах могут
существенно превысить номинальное напряжение.

Обрыв фазы при симметричной нагрузке в схеме без нулевого провода
При обрыве, например, фазы А сопротивления RA и RB оказываются
соединёнными последовательно и к ним приложено линейное напряжение UBC.
Напряжение на каждом из сопротивлений составляет 3 / 2 от фазного напряжения в
нормальном режиме. Нулевая точка нагрузки на векторной диаграмме напряжений
смещается на линию ВС, и при RB = RC она находится точно в середине отрезка ВС

Аварийный режим при соединении звездой с нейтральным проводом в случае обрыва одной из фаз при целой нейтрали. Схема аварийного случая. Векторные диаграммы токов и напряжений. Последствия аварийного случая.
Обрыв фазы при симметричной нагрузке в схеме с нулевым проводом
При обрыве провода, например, в фазе А ток этой фазы становится равным нулю,
напряжения и токи в фазах В и С не изменяются, а в нулевом проводе появляется ток
IN = IB + IC.Он равен току, который до обрыва протекал в фазе А (рис. 8.4.2).

Аварийный режим при соединении звездой с нейтральным проводом в случае короткого замыкания одной из фаз при целой нейтрали. Схема аварийного случая. Векторные диаграммы токов и напряжений. Последствия аварийного случая
При коротком замыкании фазы нагрузки в схеме с нулевым проводом ток в этой
фазе становится очень большим (теоретически бесконечно большим) и это приводит к
аварийному отключению нагрузки защитой. В схеме без нулевого провода при
замыкании, например, фазы А, нулевая точка нагрузки смещается в точку «А» генератора.
Тогда к сопротивлениям фаз В и С прикладываются линейные напряжения. Токи в этих
фазах возрастают в 3 раз, а ток в фазе А – в 3 раза (рис. 8.4.4).
Короткие замыкания между линейными проводами и в той и в другой схеме
приводят к аварийному отключению нагрузки.

Аварийный режим при соединении треугольником в случае короткого замыкания одной из фаз. Схема аварийного случая. Векторные диаграммы токов и напряжений. Последствия аварийного случая.
Аварийные режимы трёхфазной
цепи при соединении нагрузки в треугольник
При коротких замыканиях в фазах нагрузки или между линейными проводами токи
резко возрастают и происходит аварийное отключение установки защитой.
Обрывы фаз или линейных проводов при соединении нагрузки в треугольник не
приводят к перегрузкам по токам или напряжениям, как это иногда случается при
соединении нагрузки в звезду.
При обрыве одной фазы нагрузки (рис. 8.5.1) ток этой фазы становится равным
нулю, а в оставшихся двух фазах ток не меняется. Два линейных тока уменьшаются в 3
раз, т. е. становятся равными фазному току, а третий остаётся неизменным.

Аварийный режим при соединении треугольником в случае обрыва одного из проводов линии. Схема аварийного случая. Векторные диаграммы токов и напряжений. Последствия аварийного случая.
При обрыве линейного провода (например, В) фазные сопротивления RAB и RBC
оказываются соединёнными последовательно и включёнными параллельно с
сопротивлением RCA на напряжение UCA (рис. 8.5.2). Цепь фактически становится

70 Расчёт мощности в трёхфазных цепях, как для звезды, так и для треугольника. Расчёт для симметричных и несимметричных схем. Схемы с двумя и тремя ваттметрами. Их вид и использование.
Измерение активной мощности в трехфазных цепях производят с помощью трех, двух или одного ваттметров, используя различные схемы их включения. Схема включения ваттметров для измерения активной мощности определяется схемой сети (трех- или четырехпроводная), схемой соединения фаз приемника (звезда или треугольник), характером нагрузки (симметричная или несимметричная), доступностью нейтральной точки.
При несимметричной нагрузке в четырехпроводной цепи активную мощность измеряют тремя ваттметрами (рис. 3.18), каждый из которых измеряет мощность одной фазы – фазную мощность.
Активная мощность приемника определяют по сумме показаний трех ваттметров
Соединение в звезду без нулевого провода
Рассмотрим случай, когда к трехфазной цепи, соединенной звездой без нулевого провода, приложена несимметричная система линейных напряжений , , (рис. 6.29). Требуется определить токи , ,
 |
| Рис. 6.29 |

. Очевидно, для их определения достаточно знать фазные напряжения нагрузки. Чтобы их определить, воспользуемся законами Кирхгофа:
 ; | (6.4) |
 | |
 |
из которых следует:
 | (6.5) |
 | (6.6) |
По закону Ома с учетом уравнений (6.4), (6.5) фазные токи:
 | (6.7) |
Подставив значения токов из (6.7) в уравнение (6.4), получим уравнение с одним неизвестным:

,
из которого находим
 . | (6.8) |
Аналогичным образом можно получить другие фазные напряжения:
 ;  , | (6.9) |
хотя их проще найти по формулам (6.3) и (6.4). По фазным напряжениям легко определить токи.
Нужно отметить, что линейные напряжения задают обычно только по величине (действующие значения). Для определения комплексных значений в этом случае треугольник линейных напряжений располагают на комплексной плоскости таким образом, чтобы один вектор был направлен по оси действительных чисел. После этого из анализа геометрии топографической векторной диаграммы определяют начальные фазы других линейных напряжений.

На топографической диаграмме должно быть указано положение нейтральной точки 0'. Ее положение может быть определено по значению одного из фазных напряжений, например . Рассмотрим некоторые частные случаи.
1. Обрыв фазы в звезде без нулевого провода (рис. 6.30, а). В данном случае положение нулевой точки не определяется генератором, поэтому целесообразно вначале построить диаграмму токов.
Поскольку , то . Фактически сопротивления и обтекаются одним током, но в соответствии с указанными положительными направлениями следует считать, что токи и находятся в противофазе. Их сумма равна нулю (диаграмма на рис. 6.30 , б). При этом

.
 а) |  б) |
 в) | |
| Рис. 6.30 |
Векторная диаграмма напряжений (рис. 6.30 , в)строится по известным линейным напряжениям и заданным проводимостям фаз. Если предположить, что или , то напряжения на фазах нагрузки составляет:

;

.
Напряжение на разомкнутых зажимах

.
2. Рассмотрим другой пример, когда обрыв в фазе C (рис. 6.31,а), а нагрузка фаз имеет разный характер (активное сопротивление и емкость), причем r = xC = 1 Ом. Линейное напряжение симметричного источника В. Требуется определить фазные напряжения , , .
 а) |  б) |
| Рис. 6.31 |
Примем, что вектор направлен по оси действительных чисел, то есть В, тогда В, В. Проводимости ветвей , , . Согласно формулам (6.6) и (6.7) фазные напряжения определяются выражениями:

В;

В;

Напряжения можно определить из анализа геометрии топографической векторной диаграммы напряжений. Рассчитав сначала токи

А,
построим из точки 0' на плоскости векторы:

В;

В.

Затем строим векторы линейных напряжений. Напряжение определяется как вектор, проведенный из точки 0' в точку C. Его аргумент равен 90°, а модуль – сумме высот верхнего и нижнего треугольников.
3. Короткое замыкание в звезде без нулевого провода. Сначала рассмотрим цепь на рис. 6.32 и определим как изменятся токи симметричной звезды без нулевого провода при коротком замыкании фазы B0', если в симметричном режиме ток был равен I .
 | Из схемы видно, что при коротком замыкании фазы B потенциал точки B симметричного генератора подается в точку 0' нагрузки. Напряжения других фаз A и B, а также токи в этих фазах увеличиваются в  раз:  . Ток короткого замыкания фазы можно определить по векторной диаграмме. |
| Рис. 6.32 |
На диаграмме напряжений (рис. 6.33, а) точка 0' смещается в точку B, положение которой жестко задано симметричным источником. Угол между фазными напряжениями и равен 60º. Поскольку углы сдвига в фазах одинаковы, между токами и сохраняется тот же угол 60º (рис. 6.33, б). При сложении токов по первому закону Кирхгофа

 а) |  б) |
| Рис. 6.33 |
вектор оказывается лежащим против угла 120º, поэтому он в раз больше двух других фазных токов:

.
 a) |  б) |
 | в) |
| Рис. 6.34 |
В несимметричной схеме (рис. 6.34, а) диаграмма напряжений (рис. 6.34, б) сохраняется, но соотношение токов изменится (рис. 6.34, в), при этом ток короткого замыкания оказывается равным по величине токам двух неповрежденных фаз.
Соединение треугольником
Необходимо заметить, что обмотки генераторов не соединяются в треугольник, так как при таком соединении даже незначительная несимметрия фазных э.д.с. приводит к появлению значительных уравнительных токов, что не допустимо по условиям эксплуатации.
В качестве источников, фазные э.д.с. которых соединены в треугольник, можно использовать трехфазный трансформатор с вторичной обмоткой, соединенной в треугольник. Трансформаторы в трехфазных цепях могут иметь не только одинаковые, но и разные схемы соединений магнитосвязанных обмоток.
Разные схемы соединений позволяют согласовать между собой трехфазные системы с различными по величине или (и) фазе напряжениями.
Трехфазная нагрузка, присоединенная к сети, также может быть соединена в треугольник. При несимметричных режимах работы приемника, соединенного в треугольник, фазные и соответственно линейные токи получаются неравными, однако при любой несимметрии сумма комплексных значений линейных токов равна нулю:


.
Задача расчета цепи при несимметричной нагрузке, соединенной в треугольник, решается просто, поскольку по известным линейным напряжениям можно найти фазные токи. После этого по первому закону Кирхгофа определяют линейные токи. Рассмотрим ряд частных случаев.
1.Обрыв фазы в треугольнике (рис. 6.35, а). Топографическая диаграмма напряжений в этом случае (рис. 6.35, б) не деформирована. Структура векторной диаграммы токов точно такая же, как и в симметричном
 а) |  б) |
 в) |  г) |
| Рис.6.35 |
режиме, деформирована лишь форма диаграммы. Из одной точки строится звезда фазных токов (рис. 6.35, в и г). Так как , можно считать, что конец и начало этого вектора находятся в одной точке, а именно в точке, где начинаются все фазные токи. Концы векторов этих фазных токов замыкаются линейными токами , и , направление ориентации которых известно (как в симметричном режиме). Ток направлен во всех вариантах (рис. 6.35, в и г) из конца вектора в конец вектора , ток – из конца вектора в точку расхождения фазных токов и , поскольку в этой точке начинается и заканчивается нулевой вектор тока . Из этой же точки начинается вектор , направленный в конец вектора . Комплексы токов и находятся в противофазе, хотя фактически это один и тот же ток. Это является результатом специфического выбора направлений токов в треугольнике. Токи и физически одинаковы (см. схему на рис. 6.35, а) и изображаются одинаковыми векторами, так как совпадают условные положительные направления токов.

На рис. 6.35, в принято , тогда величина

.

Тупой угол треугольника равен 120°, следовательно, .
На рис. 6.35, г, когда

,

имеем правильный треугольник токов, все токи по величине равны .
 а) |  б) |
 | в) |
 г) | |
| Рис. 6.36 |
На рис. 6.36, в в таком порядке построены диаграммы для активной нагрузки . Здесь точка c лежит на середине вектора , так как . Величина равна высоте правильного треугольника генераторных напряжений. Величина в два раза меньше тока , линейные токи составляют . Один и тот же ток представлен на схеме цепи двумя условными положительными направлениями токов, соответственно на диаграмме рис. 6.36, в им соответствуют два вектора ( и ), которые находятся в противофазе.
 а) |  б) | |
 в) |  | г) |
| Рис. 6.37 |
На рис. 6.37, г построены диаграммы для случая, когда

.
3. Короткое замыкание фазы в примыкающем линейном проводе. Положение всех точек схемы (рис. 6.37 , а) на топографической диаграмме задается напряжениями генератора (рис. 6.37 , б). Причем потенциалы точек C, c, a одинаковы.
Диаграмма токов (рис. 6.37 , в) строится с соблюдением обычных правил, начиная с токов , , , которые могут быть рассчитаны и ориентированы по соответствующим напряжениям. Векторы и строятся из одной точки, а ток – так, чтобы его конец совпадал с концом вектора . Начало вектора определит положение конца вектора , а начало этого вектора совпадает с началом векторов и . Затем структура диаграммы дополняется недостающими токами и . Величины , и можно определить из геометрии диаграммы.
На рис. 6.37, в построена диаграмма токов для . Здесь , . Величина может быть рассчитана по теореме косинусов или определяется длиной вектора диаграммы в соответствующем масштабе.
Рассмотрим случай смешанной нагрузки. Пусть , , при . Из диаграммы на рис. 6.37, г, построенной в том же порядке, следует интересное заключение: вектор , находящийся между концами векторов и , равен нулю. Все остальные токи, кроме тока , по величине одинаковы:

.
 | Ток короткозамкнутой фазы находят по теореме косинусов. 4. Определить ток  при обрыве линии  в заданной схеме (рис. 6.38) с симметричным источником, если задано:  ;  Ом;  . При принятых условных положительных направлениях по закону Ома |
| Рис. 6.38 |

А, а
А.
По первому закону Кирхгофа находим токи:

А.

А.
 |
| Рис. 6.39 |
Из диаграммы (рис. 6.39) следует:
 |   ;  В. 5. Определить ток при обрыве фазы в заданной схеме (рис. 6.40) с симметричным источником, если задано:  . По закону Ома находим токи: |
| Рис. 6.40 |
А;
А.
По первому закону Кирхгофа

,

А.
 |
| Рис. 6.41 |
Векторная диаграмма напряжений и токов показана на рис. 6.41.
В приведенных примерах трехфазная цепь рассчитывается, как обыкновенная разветвленная схема. Особенность лишь в том, что используются общепринятые для трехфазных цепей условные положительные направления токов. Этим направлениям соответствует и структура векторных диаграмм.
Аварийные режимы трехфазной цепи при соединении нагрузки в треугольник
Цель работы: Экспериментально исследовать аварийные режимы трёхфазной цепи при соединении нагрузки в треугольник.
Краткая теория
При коротких замыканиях в фазах нагрузки или между линейными проводами токи резко возрастают и происходит аварийное отключение установки защитой.
Обрывы фаз или линейных проводов при соединении нагрузки в треугольник не приводят к перегрузкам по токам или напряжениям, как это иногда случается при соединении нагрузки в звезду.
При обрыве одной фазы нагрузки (рисунок 1) ток этой фазы становится равным нулю, а в оставшихся двух фазах ток не меняется. Два линейных тока уменьшаются в раз, т. е. становятся равными фазному току, а третий остаётся неизменным.
При обрыве линейного провода (например, В) фазные сопротивления RAB и RBC оказываются соединёнными последовательно и включёнными параллельно с сопротивлением RCA на напряжение UCA (рисунок 2). Цепь фактически становится однофазной.
При одновременном обрыве линейного провода и одной фазы нагрузки цепь также становится однофазной (рисунок 3 и 4).
Порядок выполнения работы
· Собрать цепь согласно схеме (рисунок 5) с сопротивлениями фаз RAВ=RBС=RCА=1кОм и измерить линейные и фазные токи в симметричном режиме.
· Измерить фазные и линейные токи во всех режимах, указанных в таблице 1. (Измерения токов можно производить одним – двумя амперметрами, переключая их из одной фазы в другую, либо виртуальными приборами).

· По экспериментальным данным построить векторные диаграммы токов для каждого аварийного случая в выбранном масштабе.
| Режим | IAB, мА | IBC, мА | ICA, мА | IA, мА | IB, мА | IC, мА |
| Симметричный режим, Rф=1 кОм | ||||||
| Обрыв фазы АВ нагрузки | ||||||
| Обрыв линейного провода А | ||||||
| Обрыв фазы АВ и линии С | ||||||
| Обрыв фазы АВ и линии А |
Контрольные вопросы и задачи:
1 Как изменятся фазные и линейные токи трехфазного симметричного потребителя, соединенного треугольником при обрыве фазы, линейного провода?
2 Как изменится сила тока в неповрежденной фазе при обрыве двух фаз приемника, соединенного треугольником?
3 Почему короткое замыкание одной из фаз трехфазного потребителя, соединенного треугольником является аварийным режимом?
1 Электротехника / Под ред. В.Г. Герасимова.- М.: Высш. шк., 1986.
2 Касаткин А.С., Немцов М.В. Электротехника. –М.: Высш. шк., 2003.
3 Борисов Ю.М., Липатов Д.Н., Зорин Ю.Н. Электротехника. -М.:
4 Волынский Б.А. и др. Электротехника.-М.: Энергоатомиздат, 1987.
5 Рекус Г.Г. Сборник задач по электротехнике и основам электроники.
- М.: Высшая школа, 1991.
Лабораторная работа 1………………………………..…13
Лабораторная работа 2…………………………………..18
Лабораторная работа 3…………………………………..22
Лабораторная работа 4…………………………………..27
Лабораторная работа 5…………………………………..32
Лабораторная работа 6…………………………………..37
Лабораторная работа 7…………………………………..44
Лабораторная работа 8…………………………………..48
Лабораторная работа 9…………………………………..52
Список литературы…………………. 56
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
Казахский национальный технический университет имени К.И. Сатпаева
Кафедра «Электротехника»
СОГЛАСОВАНО УТВЕРЖДАЮ
Заведующий кафедрой Председатель научно-
«Электротехника» методического совета,
директор института ИИТ
_____________Н.К. Кожаспаев. ____________М.Ш. Байбатшаев
Исследование аварийных режимов трехфазной цепи при соединении нагрузки в «звезду»
Цель работы: Экспериментально исследовать аварийные режимы трёхфазной цепи при соединении нагрузки в «звезду».
Краткая теория
Аварийные режимы возникают при коротких замыканиях в нагрузке или в линиях и при обрыве проводов. Рассмотрим некоторые типичные аварийные режимы.
Обрыв нейтрального провода при несимметричной нагрузке
В симметричном режиме IN = 0, поэтому обрыв нейтрального провода не приводит к изменению токов и напряжений в цепи и такой режим не является аварийным. Однако, при несимметричной нагрузке IN ¹ 0, поэтому обрыв нейтрали приводит к изменению всех фазных токов и напряжений. На векторной диаграмме напряжений точка «0» нагрузки, совпадающая до этого с точкой «N» генератора, смещается таким образом, чтобы сумма фазных токов оказалась равной нулю (рисунок 1). Напряжения на отдельных фазах могут существенно превысить номинальное напряжение.
Обрыв фазы при симметричной нагрузке в схеме с нулевым проводом
При обрыве провода, например, в фазе А ток этой фазы становится равным нулю, напряжения и токи в фазах В и С не изменяются, а в нулевом проводе появляется ток I N = I B + I C . Он равен току, который до обрыва протекал в фазе А (рисунок 2).
Обрыв фазы при симметричной нагрузке в схеме без нулевого провода
При обрыве, например, фазы А сопротивления RВ и RС оказываются соединёнными последовательно и к ним приложено линейное напряжение UBC. Напряжение на каждом из сопротивлений составляет от фазного напряжения в нормальном режиме. Нулевая точка нагрузки на векторной диаграмме напряжений смещается на линию ВС и при RB = RC находится точно в середине отрезка ВС (рисунок 3).
Короткие замыкания
При коротком замыкании фазы нагрузки в схеме с нулевым проводом ток в этой фазе становится очень большим (теоретически бесконечно большим) и это приводит к аварийному отключению нагрузки защитой. В схеме без нулевого провода при замыкании, например, фазы А, нулевая точка нагрузки смещается в точку «А» генератора. Тогда к сопротивлениям фаз В и С прикладываются линейные напряжения. Токи в этих фазах возрастают в раз, а ток в фазе А – в 3 раза (рисунок 4).
Короткие замыкания между линейными проводами и в той и в другой схеме приводят к аварийному отключению нагрузки.
Порядок выполнения работы
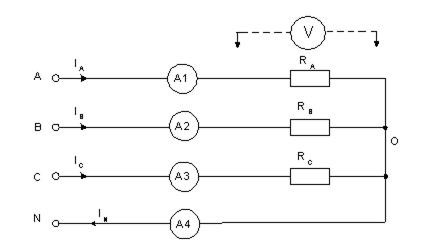
· Собрать цепь согласно схеме (рисунок 5) с сопротивлениями фаз RA=RB=RC=1кОм. (Измерения токов можно производить одним-двумя амперметрами, переключая их из одной фазы в другую, либо виртуальными приборами).
· Убедиться, что обрыв (отключение) нейтрали не приводит к изменению фазных токов.
· Убедиться, что в схеме с нулевым проводом происходит отключение источника защитой при коротких замыканиях как в фазах нагрузки, так и между линейными проводами.
· Убедиться, что в схеме без нулевого провода короткое замыкание в фазе нагрузки не приводит к отключению, а при коротком замыкании между линейными проводами установка отключается.
· Снять измерения токов и напряжений всех величин, указанных в таблице 1 в различных режимах и по экспериментальным данным построить векторные диаграммы для каждого случая в выбранном масштабе.
| Режим | UA, B | UB, B | UC, B | UnN, B | IA, мА | IB, мА | IC, мА | IN, мА |
| RA=1 кОм RB=680 Ом RC=330 Ом Обрыв нейтрали | ||||||||
| RA=RB=RC=1 кОм Схема с нейтралью Обрыв фазы А | ||||||||
| RA=RB=RC=1 кОм Схема без нейтрали Обрыв фазы А | ||||||||
| RA=RB=RC=1 кОм Схема без нейтрали к. з. фазы А |
Контрольные вопросы и задачи:
1 Как изменятся напряжения и токи при отключении нейтрального провода в схеме «звезда» для симметричной и несимметричной нагрузки?
2 Как изменятся напряжения и токи при коротком замыкании фазы в схеме«звезда» с нулевым проводом и в схеме без нулевого провода?
3 Как изменится мощность трехфазной нагрузки при обрыве фазы в схеме с нулевым проводом и без него?
Аварийные режимы работы трехфазных цепей при соединении звездой
Для соединения трехфазной цепи в звезду возможны следующие аварийные режимы работы:
1) обрыв фазы (рис. 1);
2) обрыв нулевого провода (рис2);
3) короткое замыкание фазы при обрыве нуля (рис. 3.).
4) обрыв фазы и нуля, рис. 3.

1) При обрыве фазы А , работа нагрузкой не совершается, а остальные нагрузки ( ) свои режимы работы не изменят (рис1). : .

Если нагрузки связаны и является одним целым, то этот режим будет аварийным. Так, если эта нагрузка – асинхронный двигатель, то он будет в аварийном режиме и нулевой провод будет нагружен дополнительно (рис. 4):
2) Обрыв нулевого провода не всегда вызывает аварию в трехфазных цепях. Если нагрузка симметрична, то обрыв нулевого провода не изменит токов нагрузок, так как для симметричной нагрузки
Для несимметричных нагрузок , и поэтому такой режим может вызвать аварию.
Для того чтобы показать это, используем метод двух узлов:

Напряжение (рис. 5) не равно нулю, если нагрузки несимметричны. Фазные токи также будут неодинаковыми.
3) При коротком замыкании фазы А и обрыве нуля напряжение этой фазы равно нулю: .
Нагрузка фазы В увеличится в раз: .
Аналогично и в фазе С:
будет увеличен по отношению к исходному в раз.
4) Обрыв фазы и нулевого провода дает:
В оставшихся фазах токи будут одинаковыми, а напряжения на них будут зависеть от сопротивлений нагрузок .
Обрыв фазы при симметричной нагрузке в схеме с нулевым проводом
IN = IB + IC. Он равен току, который до обрыва протекал в фазе А (рис. 8.4.2).

Обрыв фазы при симметричной нагрузке в схеме без нулевого провода

При обрыве, например, фазы А сопротивления RAи RBоказываются соединёнными последовательно и к ним приложено линейное напряжение UBC. Напряжение на каждом из сопротивлений составляетот фазного напряжения в нормальном режиме. Нулевая точка нагрузки на векторной диаграмме напряжений смещается на линию ВС и при RB= RCнаходится точно в середине отрезка ВС (рис.8.4.3

Короткие замыкания

При коротком замыкании фазы нагрузки в схеме с нулевым проводом ток в этой фазе становится очень большим (теоретически бесконечно большим) и это приводит к аварийному отключению нагрузки защитой. В схеме без нулевого провода при замыкании, например, фазы А, нулевая точка нагрузки смещается в точку «А» генератора. Тогда к сопротивлениям фаз В и С прикладываются линейные напряжения. Токи в этих фазах возрастают в раз, а ток в фазе А – в 3 раза (рис. 8.4.4).
Короткие замыкания между линейными проводами и в той и в другой схеме приводят к аварийному отключению нагрузки.

8.4.2. Экспериментальная часть Задание
Экспериментально исследовать аварийные режимы трёхфазной цепи при соединении нагрузки в звезду.
Порядок выполнения работы
Соберите цепь цепь согласно схеме (рис.8.4.5) с сопротивлениями фаз RA=RB=RC=1кОм.Измерения токов можно производить одним – двумя амперметрами, переключая их из одной фазы в другую, либо виртуальными приборами.

Убедитесь, что обрыв (отключение) нейтрали не приводит к изменению фазных токов.
Убедитесь, что в схеме с нулевым проводом происходит отключение источника защитой при коротких замыканиях как в фазах нагрузки, так и между линейными проводами.
Убедитесь, что в схеме без нулевого провода короткое замыкание в фазе нагрузки не приводит к отключению, а при коротком замыкании между линейными проводами установка отключается.
Проделайте измерения токов и напряжений всех величин, указанных в табл. 8.4.1 в различных режимах и по экспериментальным данным постройте векторные диаграммы для каждого случая в выбранном масштабе.
Читайте также:

