Жидкость течет по трубе переменного сечения сравнить давление p и скорость течения жидкости в точках
Обновлено: 07.07.2024
Жидкость течет по трубе переменного сечения сравнить давление p и скорость течения жидкости в точках
В этом параграфе мы применим закон сохранения энергии к движению жидкости или газа по трубам. Движение жидкости по трубам часто встречается в технике и быту. По трубам водопровода подается вода в городе в дома, к местам ее потребления. В машинах по трубам поступает масло для смазки, топливо в двигатели и т. д. Движение жидкости по трубам нередко встречается и в природе. Достаточно сказать, что кровообращение животных и человека — это течение крови по трубкам — кровеносным сосудам. В какой-то мере течение воды в реках тоже является разновидностью течения жидкости по трубам. Русло реки — это своеобразная труба для текущей воды.
Как известно, неподвижная жидкость в сосуде согласно закону Паскаля передает внешнее давление по всем направлениям и во все точки объема без изменения. Однако, когда жидкость течет без трения по трубе, площадь поперечного сечения которой на разных участках различна, давление оказывается неодинаковым вдоль трубы. Выясним, почему давление в движущейся жидкости зависит от площади поперечного сечения трубы. Но сначала ознакомимся с одной важной особенностью всякого потока жидкости.
Предположим, что жидкость течет по горизонтально расположенной трубе, сечение которой в разных местах различное, например по трубе, часть которой показана на рисунке 207.
Если бы мы мысленно провели несколько сечений вдоль трубы, площади которых соответственно равны и измерили бы количество жидкости, протекающей через каждое из них за какой-то промежуток времени то мы обнаружили бы, что через каждое сечение протекло одно и то же количество жидкости. Это значит, что вся та жидкость, которая за время проходит через первое сечение, за такое же время проходит и через третье сечение, хотя оно по площади значительно меньше, чем первое. Если бы это было не так и через сечение площадью за время проходило, например, меньше жидкости, чем через сечение площадью то избыток жидкости должен был бы где-то накапливаться. Но жидкость заполняет всю трубу, и накапливаться ей негде.
Как же может жидкость, протекшая через широкое сечение, успеть за такое же время «протиснуться» через узкое? Очевидно, что для этого при прохождении узких частей трубы скорость движения должна быть больше, и как раз во столько раз, во сколько раз площадь сечения меньше.
Действительно, рассмотрим некоторое сечение движущегося столба жидкости, совпадающее в начальный момент времени с одним из сечений трубы (рис. 208). За время эта площадка переместится на расстояние которое равно где — скорость течения жидкости. Объем V жидкости, протекшей через сечение трубы, равен произведению площади этого сечения на длину
В единицу же времени протекает объем жидкости —
Объем жидкости, протекающей в единицу времени через сечение трубы, равен произведению площади поперечного сечения трубы на скорость течения.
Как мы только что видели, этот объем должен быть одним и тем же в разных сечениях трубы. Поэтому, чем меньше сечение трубы, тем больше скорость движения.
Сколько жидкости проходит через одно сечение трубы за некоторое время, столько же ее должно пройти за такое
же время через любое другое сечение.
При этом мы считаем, что данная масса жидкости всегда имеет один и тот же объем, что она не может сжаться и уменьшить свой объем (о жидкости говорят, что она несжимаема). Хорошо известно, например, что в узких местах реки скорость течения воды больше, чем в широких. Если обозначить скорость течения жидкости в сечениях площадями через то можно написать:
Отсюда видно, что при переходе жидкости с участка трубы с большей площадью сечения на участок с меньшей площадью сечения скорость течения увеличивается, т. е. жидкость движется с ускорением. А это по второму закону Ньютона означает, что на жидкость действует сила. Что это за сила?
Этой силой может быть только разность между силами давления в широком и узком участках трубы. Таким образом, в широком участке давление жидкости должно быть больше, чем в узком участке трубы.
Это же следует из закона сохранения энергии. Действительно, если в узких местах трубы увеличивается скорость движения жидкости, то увеличивается и ее кинетическая энергия. А так как мы приняли, что жидкость течет без трения, то этот прирост кинетической энергии должен компенсироваться уменьшением потенциальной энергии, потому что полная энергия должна оставаться постоянной. О какой же потенциальной энергии здесь идет речь? Если труба горизонтальна, то потенциальная энергия взаимодействия с Землей во всех частях трубы одна и та же и не может измениться. Значит, остается только потенциальная энергия упругого взаимодействия. Сила давления, которая заставляет жидкость течь по трубе, — это и есть упругая сила сжатия жидкости. Когда мы говорим, что жидкость несжимаема, то имеем лишь в виду, что она не может быть сжата настолько, чтобы заметно изменился ее объем, но очень малое сжатие, вызывающее появление упругих сил, неизбежно происходит. Эти силы и создают давление жидкости. Вот это сжатие жидкости и уменьшается в узких частях трубы, компенсируя рост скорости. В узких местах труб давление жидкости должно быть поэтому меньше, чем в широких.
В этом состоит закон, открытый петербургским академиком Даниилом Бернулли:
Давление текущей жидкости больше в тех сечениях потока, в которых скорость ее движения меньше, и,
наоборот, в тех сечениях, в которых скорость больше, давление меньше.
Как это ни покажется странным, но когда жидкость «протискивается» через узкие участки трубы, то ее сжатие не увеличивается, а уменьшается. И опыт хорошо это подтверждает.
Если трубу, по которой течет жидкость, снабдить впаянными в нее открытыми трубками — манометрами (рис. 209), то можно будет наблюдать распределение давления вдоль трубы. В узких местах трубы высота столба жидкости в манометрической трубке меньше, чем в широких. Это означает, что в этих местах давление меньше. Чем меньше сечение трубы, тем больше в ней скорость течения и меньше давление. Можно, очевидно, подобрать такое сечение, в котором давление равно внешнему атмосферному давлению (высота уровня жидкости в манометре будет тогда равна нулю). А если взять еще меньшее сечение, то давление жидкости в нем будет меньше атмосферного.
Такой поток жидкости можно использовать для откачки воздуха. На этом принципе действует так называемый водоструйный насос. На рисунке 210 изображена схема такого насоса. Струю воды пропускают через трубку А с узким отверстием на конце. Давление воды у отверстия трубы меньше атмосферного. Поэтому
газ из откачиваемого объема через трубку В втягивается к концу трубки А и удаляется вместе с водой.
Все сказанное о движении жидкости по трубам относится и к движению газа. Если скорость течения газа не слишком велика и газ не сжимается настолько, чтобы изменялся его объем, и если, кроме того, пренебречь трением, то закон Бернулли верен и для газовых потоков. В узких частях труб, где газ движется быстрее, давление его меньше, чем в широких частях, и может стать меньше атмосферного. В некоторых случаях для этого даже не требуется трубы.
Можно проделать простой опыт. Если дуть на лист бумаги вдоль его поверхности, как показано на рисунке 211, можно увидеть, что бумага станет подниматься вверх. Это происходит из-за понижения давления в струе воздуха над бумагой.
Такое же явление имеет место при полете самолета. Встречный поток воздуха набегает на выпуклую верхнюю поверхность крыла летящего самолета, и за счет этого происходит понижение давления. Давление над крылом оказывается меньше, чем давление под крылом. Именно поэтому возникает подъемная сила крыла.
Упражнение 62
1. Допустимая скорость течения нефти по трубам равна 2 м/сек. Какой объем нефти проходит через трубу диаметром 1 м в течение 1 ч?
2. Измерьте количество воды, вытекающей из водопроводного крана за определенное время Определите скорость течения воды, измерив диаметр трубы перед краном.
3. Каким должен быть диаметр трубопровода, по которому должно протекать воды в час? Допустимая скорость течения воды 2,5 м/сек.
Гидроаэродинамика
Движение жидкостей или газов представляет собой сложное явление. Для его описания используются различные упрощающие предположения (модели). В простейшей модели жидкость (или газ) предполагаются несжимаемыми и идеальными (то есть без внутреннего трения между движущимися слоями). При движении идеальной жидкости не происходит превращения механической энергии во внутреннюю, поэтому выполняется закон сохранения механической энергии .
Следствием этого закона для стационарного потока идеальной и несжимаемой жидкости является уравнение Бернулли (1738 г.). Стационарным принято называть такой поток жидкости, в котором не образуются вихри. В стационарном потоке частицы жидкости перемещаются по неизменным во времени траекториям, которые называются линиями тока . Опыт показывает, что стационарные потоки возникают только при достаточно малых скоростях движения жидкости. Рассмотрим стационарное движение идеальной несжимаемой жидкости по трубе переменного сечения (рис. 1). Различные части трубы могут находиться на разных высотах.
Это и есть уравнение Бернулли . Из него следует, что сумма
остается неизменной вдоль всей трубы. В частности, для горизонтально расположенной трубы (h1 = h2) уравнение Бернулли принимает вид:
Величина p – статическое давление в жидкости. Оно может быть измерено с помощью манометра, перемещающегося вместе с жидкостью. Практически давление в разных сечениях трубы измеряется с помощью манометрических трубок, вставленных через боковые стенки в поток жидкости, так чтобы нижние концы трубок были перпендикулярны скоростям частиц жидкости (рис. 2). Из уравнения Бернулли следует:
| Давление в жидкости, текущей по горизонтальной трубе переменного сечения, больше в тех сечениях потока, в которых скорость ее движения меньше, и наоборот, давление меньше в тех сечениях, в которых скорость больше. |
| Рисунок 2. Измерение давления в потоке жидкости с помощью манометров. v1 < v2 < v3; h1 > h2 > h3. |
Если сечение потока жидкости достаточно велико, то уравнение Бернулли следует применять к линиям тока , то есть линиям, вдоль которых перемещаются частицы жидкости при стационарном течении. Например, при истечении идеальной несжимаемой жидкости из отверстия в боковой стенке или дне широкого сосуда линии тока начинаются вблизи свободной поверхности жидкости и проходят через отверстие (рис. 3).
| Рисунок 3. Истечение жидкости из широкого сосуда. |
Поскольку скорость жидкости вблизи поверхности в широком сосуде пренебрежимо мала, то уравнение Бернулли принимает вид:
где p0 – атмосферное давление, h – перепад высоты вдоль линии тока. Таким образом,
Это выражение для скорости истечения называют формулой Торричелли . Скорость истечения идеальной жидкости из отверстия в сосуде такая же, как и при свободном падении тела с высоты h без начальной скорости. В отличие от жидкостей, газы могут сильно изменять свой объем. Расчеты показывают, что сжимаемостью газов можно пренебречь, если наибольшие скорости в потоке малы по сравнению со скоростью звука в этом газе. Таким образом, уравнение Бернулли можно применять к достаточно широкому классу задач аэродинамики. Одной из таких задач является изучение сил, действующих на крыло самолета.
Строгое теоретическое решение этой задачи чрезвычайно сложно, и обычно для исследования сил применяются экспериментальные методы. Уравнение Бернулли позволяет дать лишь качественное объяснение возникновению подъемной силы крыла. На рис. 4 изображены линии тока воздуха при обтекании крыла самолета. Из-за специального профиля крыла и наличия угла атаки , то есть угла наклона крыла по отношению к набегающему потоку воздуха, скорость воздушного потока над крылом оказывается больше, чем под крылом. Поэтому на рис. 4 линии тока над крылом располагаются ближе друг к другу, чем под крылом. Из уравнения Бернулли следует, что давление в нижней части крыла будет больше, чем в верхней; в результате появляется сила действующая на крыло. Вертикальная составляющая этой силы называется подъемной силой. Подъемная сила позволяет скомпенсировать силу тяжести, действующую на самолет, и тем самым она обеспечивает возможность полета тяжелых летательных аппаратов в воздухе. Горизонтальная составляющая представляет собой силу сопротивления среды.
Теория подъемной силы крыла самолета была создана Н. Е. Жуковским. Он показал, что существенную роль при обтекании крыла играют силы вязкого трения в поверхностном слое. В результате их действия возникает круговое движение ( циркуляция ) воздуха вокруг крыла (зеленые стрелки на рис. 4). В верхней части крыла скорость циркулирующего воздуха складывается со скоростью набегающего потока, в нижней части эти скорости направлены в противоположные стороны. Это и приводит к возникновению разности давлений и появлению подъемной силы. Циркуляция воздуха, обусловленная силами вязкого трения, возникает и вокруг вращающегося тела (например, цилиндра). При вращении цилиндр увлекает прилегающие слои воздуха, вызывая его циркуляцию. Если такой цилиндр установить в набегающем потоке воздуха, то возникнет сила бокового давления, аналогичная подъемной силе крыла самолета. Это явление называется эффектом Магнуса. Рис. 5 иллюстрирует обтекание вращающегося цилиндра набегающим потоком. Эффект Магнуса проявляется, например, при полете закрученного мяча при игре в теннис или футбол.
| Рисунок 5. Обтекание вращающегося цилиндра набегающим потоком воздуха. |
Итак, во многих явлениях аэродинамики существенную роль играют силы вязкого трения. Они приводят к возникновению циркулирующих потоков воздуха вокруг крыла самолета или вокруг вращающегося тела, к появлению силы сопротивления среды и т. д. Уравнение Бернулли не учитывает сил трения. Его вывод основан на законе сохранения механической энергии при течении жидкости или газа. Поэтому с помощью уравнения Бернулли нельзя дать исчерпывающего объяснения явлений, в которых проявляются силы трения. В этих случаях можно руководствоваться только качественными соображениями – чем больше скорость, тем меньше давление в потоке газа. Особенно заметно проявляются силы вязкого трения при течении жидкостей. У некоторых жидкостей вязкость настолько велика, что применение уравнение Бернулли может привести к качественно неверным результатам. Например, при истечении вязкой жидкости через отверстие в стенке сосуда ее скорость может быть в десятки раз меньше рассчитанной по формуле Торричелли. При движении сферического тела в идеальной жидкости оно не должно испытывать лобового сопротивления. Если же такое тело движется в вязкой жидкости, то возникает сила сопротивления, модуль которой пропорционален скорости v и радиусу сферы r ( закон Стокса )
Fсопр
Коэффициент пропорциональности в этой формуле зависит от свойств жидкости. Поэтому, если тяжелый шарик бросить в высокий сосуд, наполненный вязкой жидкостью (например, глицерином), то через некоторое время скорость шарика достигнет установившегося значения, которое не будет изменяться при дальнейшем движении шарика. При движении с установившейся скоростью силы, действующие на шарик (сила тяжести выталкивающая сила и сила сопротивления среды ), оказываются скомпенсированными, и их равнодействующая равна нулю.
Слободянюк А.И. Физика 10/7.11
Если по горизонтальной трубе постоянного сечения будет протекать жидкость реальная жидкость, для которой нельзя пренебречь силами вязкого трения, то давление в трубе не будет постоянным, произойдет перераспределение давления, которое будет существенно зависеть от свойств жидкости. Рассматривая проблемы возникновения сил вязкого трения, мы упоминали о такой характеристике жидкости как вязкость. Сейчас мы уточним это понятие.
Рассмотрим плоский поток жидкости, в пределах которого скорость \(
\vec \upsilon(z)\) различных слоев которого изменяется, оставаясь параллельной основанию потока (рис. 130). В реальной жидкости различные слои жидкости, имеющие разные скорости будут взаимодействовать между собой, то есть между слоями жидкости благодаря межмолекулярным взаимодействиям будут возникать силы вязкого трения – более медленный слой будет тормозить более быстрый. Важно отметить, что эти силы направлены параллельно слоям жидкости, то есть тангенциально к границе раздела (рис. 131). Величина этих сил также зависит от распределения скорости \(
\vec \upsilon(z)\) , где z - координата, ось которой направлена перпендикулярно скорости течения.
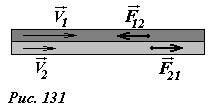
Силы вязкости определяется законом Ньютона [1] : тангенциальная сила вязкого трения между движущимися слоями жидкости приходящаяся на единицу площади соприкосновения равна
в этой формуле коэффициент пропорциональности η - полностью определяется свойствами жидкости и называется динамическим коэффициентом вязкости. Вязкость может изменяться в широких пределах, она мала для легко подвижных жидкостей, таких как вода, бензин, эфир, и велика для малоподвижных жидкостей таких как масло, мед, смола и т.д. В целом строгое понятие вязкости вполне соответствует обычным представлениям о вязких и маловязких жидкостях. Модель движущейся жидкости, в рамках которой пренебрегают вязкостью, называется идеальной жидкостью.
Обратите внимание – в случае неподвижной жидкости силы взаимодействия между слоями всегда нормальны, в движущейся жидкости появляются тангенциальные составляющие!
Важно отметить, что силы вязкости не являются консервативными, наличие этих сил, их работа приводит к переходу механической энергии в тепловую, к потерям механической энергии.
При стационарном движении жидкости трубы на нее со стороны стенок будут действовать тормозящие силы вязкого трения. Поэтому скорость движения жидкости в поперечном сечении будет различной, установится некоторое стационарное распределение скоростей – скорость максимальна в центре трубы и приближается к нулю вблизи стенок (рис. 132).
Для расчета сил вязкого трения, действующих на жидкость необходимо, прежде всего, найти распределение скоростей жидкости внутри трубы (используя закон вязкого трения), после чего можно вычислить силу сопротивления движению, расход жидкости и так далее.
Для круговой цилиндрической трубы эта задача была решена французским физиком Ж. Пуазейлем, который установил, что расход [2] жидкости пропорционален разности давлений на концах трубы Δp, четвертой степени радиуса трубы, обратно пропорционален ее длине
Q = K \frac \Delta p\) , (1)
коэффициент пропорциональности зависит от вязкости жидкости. Если поперечный профиль отличен от кругового, то формула Пуазейля несколько видоизменяется, но расход жидкости остается пропорциональным разности давлений на концах трубы
в этой формуле коэффициент пропорциональности обозначен \(
\frac\) , тогда величина R - называется гидродинамическим сопротивлением. Гидростатическое сопротивление участка трубы длиной Δl можно представить в виде R = rΔl , где r - сопротивление единицы длины трубы, зависящее от вязкости жидкости, размеров и формы поперечного сечения трубы. С увеличением площади поперечного сечения гидродинамическое сопротивление уменьшается.
Внимательно посмотрим на формулу (2) – она достойна того. Если площадь поперечного сечения трубы постоянна, то скорости движения жидкости не изменяются вдоль трубы, то есть любая частица жидкости движется с постоянной скоростью, без ускорения. Тем не менее, для того чтобы жидкость двигалась с постоянной скоростью, к ней необходимо прикладывать постоянную внешнюю силу, то есть создавать разность давлений на концах трубы. Кажущееся противоречие легко снимается, если принять во внимание силы вязкого трения, действующие между различными слоями жидкости. Фактически внешнюю силу необходимо прикладывать, чтобы преодолеть силы вязкого трения. Конечно, суммарная сила, действующая на любую часть равномерно движущейся жидкости равна нулю.
Ситуация аналогична движению тела в вязкой среде, когда на него действует сила сопротивления (рис. 133), пропорциональная скорости движения Fсопр = βυ. Если к телу приложить постоянную внешнюю силу F, то тело будет двигаться со скоростью, пропорциональной внешней приложенной силе \(
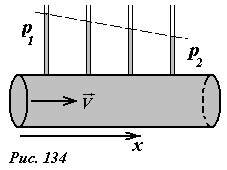
Итак, при движении вязкой жидкости по трубе внутри устанавливается распределение давлений – давление линейно падает при смещении вдоль направления движения жидкости (рис.134). Подчеркнем, что в данном случае, приложенная разность давлений является причиной движения жидкости – при стационарном движении происходит установление нужного распределения давлений вдоль трубы.
Можно сказать, что для преодоления гидростатического сопротивления R необходимо приложить разность давлений (или на сопротивлении происходит падение давления) Δp = RQ.
Направим координатную ось X вдоль трубы. Пусть в точке с координатой x = 0 давление равно p0. Применим формулу Пуазейля для слоя жидкости от x = 0 до произвольного значения координаты x. Из формулы (2) следует, что
p_0 - p(x) = QR = Qrx\) ,
где p(x) - давление жидкости в сечении с координатой x.
Таким образом, распределение давления вдоль трубы при движении вязкой жидкости представляет собой линейную зависимость p(x) = p0 - Qrx. Коэффициент наклона графика данной зависимости \(
|\frac|\) возрастает с ростом скорости течения жидкости и гидродинамического сопротивления (рис.135).
В установившемся режиме скорость [3] изменения давления вдоль трубы \(
\frac\) остается постоянной вдоль трубы. Заметим, что отношение \(
\frac\) имеет явный физический смысл. Величина F = SΔp - есть суммарная сила давления, действующая на слой жидкости толщиной Δx; следовательно, величина \(
f = \frac = \frac\) - есть суммарная сила давления, действующая на единицу объема жидкости – то есть объемная плотность силы давления.
Выделим в движущейся жидкости небольшой параллелепипед, одно из ребер которого длиной l параллельно скорости жидкости, площадь грани перпендикулярной скорости равна S (рис. 136). Пусть разность давлений между противоположными гранями этого объема равна Δp , тогда произведение ΔF = Δp'S равно суммарной силе давления на жидкость внутри выделенного объема, а величина ΔA = Δp'Sl равна работе, которую совершают силы давления внутри данного объема. Наконец, отношение \(
\frac = \Delta p\) с одной стороны разность давлений, с другой – работа сил давления, которая совершается при перетекании жидкости через данный объем.
Полученное распределение давления соответствует стационарному течению жидкости. Качественно рассмотрим процесс установления движения. Пусть длинная горизонтальная труба полностью заполнена жидкостью, с одной стороны внутри трубы расположен поршень (рис. 137). В некоторый момент времени к поршню начинают прикладывать постоянную силу. Вся жидкость в трубе сразу прийти в движение не сможет. Непосредственно перед поршнем возникнет область сжатия, которая начнет распространяться по трубе, приводя в движение все более удаленные области жидкости внутри трубы. Скорость распространения области сжатия совпадает со скоростью звука в жидкости. Наконец, по прошествии некоторого небольшого промежутка времени в трубе установится такое распределение давления, которое обеспечит постоянство скорости вдоль трубы. Именно этот установившийся режим мы и рассматриваем.
Задание для самостоятельной работы.
-
Представьте расход жидкости в виде \(
Q = \overline <\upsilon>S\) , где S - площадь поперечного сечения трубы, \(
Т. Движение жидкостей
Зависимость давления жидкости от скорости ее течения
В предыдущих параграфах были рассмотрены законы равновесия жидкостей и газов. Теперь рассмотрим некоторые явления, связанные с их движением.
Движение жидкости называют течением, а совокупность частиц движущейся жидкости потоком. При описании движения жидкости определяют скорости, с которыми частицы жидкости проходят через данную точку пространства. Если в каждой точке пространства, заполненного движущейся жидкостью, скорость не изменяется со временем, то такое движение называется установившимся, или стационарным. При стационарном течении любая частица жидкости проходит через данную точку пространства с одним и тем же значением скорости. Мы будем рассматривать только стационарное течение идеальной несжимаемой жидкости. Идеальной называют жидкость, в которой отсутствуют силы трения.
Как известно, неподвижная жидкость в сосуде, согласно закону Паскаля, передает внешнее давление ко всем точкам жидкости без изменения. Но когда жидкость течет без трения по трубе переменного поперечного сечения, давление в разных местах трубы неодинаково. Оценить распределение давлений в трубе, по которой течет жидкость, можно с помощью установки, схематически изображенной на рисунке 1. Вдоль трубы впаивают вертикальные открытые трубки-манометры. Если жидкость в трубе находится под давлением, то в манометрической трубке жидкость поднимается на некоторую высоту, зависящую от давления в данном месте трубы. Опыт показывает, что в узких местах трубы высота столбика жидкости меньше, чем в широких. Это значит, что в этих узких местах давление меньше. Чем это объясняется?
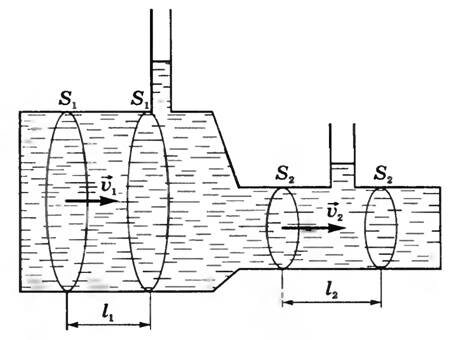
Предположим, что несжимаемая жидкость течет по горизонтальной трубе с переменным сечением (рис. 1). Выделим мысленно несколько сечений в трубе, площади которых обозначим S1 и S2. При стационар ном течении через любое поперечное сечение трубы за равные промежутки времени переносятся одинаковые объемы жидкости.
Пусть υ1 — скорость жидкости через сечение S1, υ2 — скорость жидкости через сечение S2. За время Δt объемы жидкостей, протекающих через эти сечения, будут равны:
\begin \Delta V_1 = l_1S_1 = \upsilon_1 \Delta t_1 \cdot S_1 ; \\ \Delta V_2 = l_2S_2 = \upsilon_2 \Delta t_2 \cdot S_2 . \end\)
Так как жидкость несжимаема, то ΔV1 = ΔV2. Следовательно, υ1S1 = υ2S2 или υS = const для несжимаемой жидкости. Это соотношение называется уравнением неразрывности.
Из этого уравнения \(
\frac<\upsilon_1> <\upsilon_2>= \frac\) , т.е. скорости жидкости в двух любых сечениях обратно пропорциональны площадям сечений. Это значит, что частицы жидкости при переходе из широкой части трубы в узкую ускоряются. Следовательно, на жидкость, поступающую в более узкую часть трубы, действует со стороны жидкости, еще находящейся в широкой части трубы, некоторая сила. Такая сила может возникнуть только за счет разности давлений в различных частях жидкости. Так как сила направлена в сторону узкой части трубы, то в широком участке трубы давление должно быть больше, чем в узком. Учитывая уравнение неразрывности, можно сделать вывод: при стационарном течении жидкости давление меньше в тех местах, где больше скорость течения, и, наоборот, больше в тех местах, где скорость течения меньше.
К этому выводу впервые пришел Д. Бернулли, поэтому данный закон называют законом Бернулли.
Применение закона сохранения энергии к потоку движущейся жидкости позволяет получить уравнение, выражающее закон Бернулли (приводим без вывода)\[
p_1 + \frac = p_2 + \frac\] — уравнение Бернулли для горизонтальной трубки.
Здесь p1 и p2 — статические давления, ρ — плотность жидкости. Статическое давление равно отношению силы давления одной части жидкости на другую к площади соприкосновения, когда скорость их относительного движения равна нулю. Такое давление измерил бы манометр, движущийся вместе с потоком. Неподвижная монометрическая трубка с отверстием, обращенным навстречу потоку, измерит давление \(
\frac\) имеют, с одной стороны, размерность давления, с другой — размерность объемной плотности энергии, т. е. энергии, приходящейся на единицу объема. Действительно, \(
W_k = \frac\), масса жидкости m = ρV. Если V = 1 м 3 , то \(
\frac\) — называют динамическим давлением. Это кинетическая энергия потока в единичном объеме жидкости (объемная плотность энергии).
Если трубка не горизонтальная, то надо учитывать и гидростатическое давление жидкости. Уравнение Бернулли будет иметь вид:
где h1 и h2 — высоты, на которых находятся сечения S1 и S2.
Закон Бернулли лежит в основе принципа действия многих технических устройств и приборов: водоструйного насоса, пульверизатора, форсунки карбюратора. Закон Бернулли позволяет объяснить возникновение подъемной силы крыла самолета.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 106-108.
Жидкость течет по трубе переменного сечения сравнить давление p и скорость течения жидкости в точках
Движение жидкости по трубам широко распространено в природе и технике. Например, течение рек, течение нефти по нефтепроводу, течение крови по кровеносным сосудам человека и животных и т. д.
Продувая струю воздуха между двумя шариками или листами плотной бумаги, подвешенными на нитях, можно наблюдать их взаимное притяжение. Похожее явление возникает при движении больших судов в узком канале, где суда значительно уменьшают сечение потока жидкости.
По всей видимости, давление внутри движущейся жидкости или газа уменьшается по сравнению с давлением окружающей среды.
Выясним зависимость давления жидкости от скорости её течения в трубе. Воспользуемся для этого законом сохранения механической энергии.
Рассмотрим движение идеальной жидкости в наклонном участке трубопровода, находящегося в поле земного тяготения.
Выделим мысленно некоторый элемент жидкости. Жидкость, находясь в движении, обладает кинетической энергией. Если она поднимается или опускается, то изменяется её потенциальная энергия.
Согласно закону сохранения энергии работа, совершенная над рассматриваемым элементом жидкости внешними силами, которые поддерживают движение жидкости или газа, должна быть равна изменению его полной механической энергии: = Δk + Δp.
Пусть за небольшой промежуток времени жидкость перемещается вверх и вправо. (1, 2 – поперечные сечения трубы слева и справа).
Левый участок жидкости перемещается на расстояние Δ1, за то же время правый – на Δ2.
Изменение кинетической энергии выделенного элемента жидкости равно разности кинетических энергий рассматриваемых частей:
Работа, совершаемая над выделенным элементом внешними силами, равна:
Приравнивая работу внешних сил к изменению кинетической и потенциальной энергии выделенного участка жидкости, имеем:
После преобразования получаем следующее выражение:
Это уравнение названо в честь швейцарского математика и механика Даниила Бернулли уравнением Бернулли.
Если отбросить в уравнении Бернулли слагаемое, соответствующее потенциальной энергии, то получается соотношение между давлением и скоростью жидкости, движущейся горизонтально:
Вывод очевиден: где скорость велика, там мало давление.
Давление жидкости, текущей по трубе, меньше там, где скорость её течения больше, и, наоборот, где скорость течения жидкости меньше, давление там больше.
Можно проверить справедливость уравнения Бернулли на опыте.
Через трубу переменного сечения, в которую впаяны манометрические трубки, пропускают жидкость. По высоте жидкости в манометрических трубках судят о давлении в разных сечениях трубы. На рисунке наименьшее давление – в среднем сечении трубы.
Уравнение Бернулли справедливо не только для жидкостей, но и для газов, если их сжатие мало.
Работа водоструйных насосов, автомобильных карбюраторов, пульверизаторов, водомеров и газомеров основана на уравнении Бернулли.
Уравнение Бернулли ( формула пример)
Уравнение Бернулли Статическое и динамическое давление

Силы притяжения между молекулами в жидкости больше, чем в газах, но значительно меньше, чем в твердых телах. Частицы жидкости легко взаимно смещаются и под действие тления легко перемещаются из области более высокого давления в сторону более низкого. Это называется тече нием жидкости.
Вследствие наличия сил притяжения взаимное смещение частиц жидкости сопровождается некоторым сопротивлением, которое подобно механическому трению между мелкими частицами твердого вещества и называется внутренним трением, или вязкостью, жидкости. Вязкость жидкости проявляется, например, сопротивлением при помешивании жидкости, замедлением при падении в жидкости предметов и т. д.
Рассмотрим вначале стационарное течение идеальной жидкости (идеальной называется несжимаемая жидкость, не имеющая вязкости; стационарным называется течение, при котором величина скорости в любой точке жидкости со временем не изменяется). Установим для этих условий соотношение между давлением р в жидкости, скоростью движения v ее частиц и положением их в поле силы тяжести, характеризуемое высотой Л над некоторым уровнем отсчета (рис. 2).
Уравнение Бернулли
В соответствии с законом сохранения энергии полная энергия некоторой массы m (имеющей объем V) идеальной жидкости при течении остается неизменной, так как в ней отсутствуют потери на внутреннее трение.
Соответственно для каких-либо двух положений массы т идеальной жидкости, например в точках А и Б (рис. 2):
Если предпоследнее уравнение разделить почленно на объем V жидкости, то учитывая, что m/V есть плотность ρ жидкости, получим:
p + ρgh +(ρυ 2 /2) = const.
Это и есть уравнение Бернулли.
Для движения жидкости в горизонтальных трубках силу тяжести можно не учитывать и тогда уравнение Бернулли принимает вид:
p +(ρυ 2 /2) const
Из этого уравнения следует вывод, называемый правилом Бернулли: давление невязкой жидкости, текущей по горизонтальной трубе, выше там, где скорость ее меньше, и наоборот.
Пример расчета по формуле
Рассмотрим течение жидкости по трубе с неодинаковым сечением. Течение называется непрерывным, если через любое сечение трубы в единицу времени протекает одинаковое количество (объем) жидкости. При этом скорость движения жидкости на участках трубы обратно пропорциональна площади их сечений.
Действительно не трудно доказать, что объем V0 жидкости, протекающей в единицу времени через любое сечение трубы, может быть выражен произведением площади S сечения трубы на скорость υ течения жидкости: V0=Sυ. По условию этот объем постоянен для любого сечения трубы, следовательно,
V0 = Sυ = const.
т. е. произведение скорости течения жидкости на поперечное сечение струи есть величина постоянная. Это соотношение называют уравнением неразрывности струи.
Если обозначить сечение и скорость движения на участках трубы соответственно S1 и υ1 S2 и υ2, то согласно сказанному:
Скорость течения жидкости в трубе с переменным сечением обратно пропорциональна площади этих сечений.
При этом в соответствии с правилом Бернулли на участках меньшего сечения трубы давление будет ниже, на участках большего сечения — выше (рис. , а). Поясним механизм этого явления. При переходе на участок трубы меньшего сечения (линия ab на рис. , б) частицы жидкости ускоряются, на что затрачивается часть силы Р4, создающей давление на более широком участке (по условию равновесия частиц жидкости Р1= Р2+Fу, где Р2 — сила, создающая давление на суженном участке, Fу — сила, обеспечивающая ускорение частиц).
Наоборот, при переходе на участок с большим сечением (линия cd на рис. 82, б) частицы жидкости набегают на лежащую впереди и более медленно двигающуюся массу жидкости и, затормаживаясь, создают дополнительную силу Fт, повышающую давление на более широком участке (аналогично P3=P2 + Fт).
Можно подобрать условия, при которых давление жидкости в сужен ном участке трубы станет ниже атмосферного и тогда в этом месте струя будет обладать всасывающим действием. Всасывающее действие струи газа, пара или воды, выходящей из суженного отверстия с большой скоростью, используется в ряде приборов, применяемых в медицинской практике (ингалятор, водоструйный насос и др.).
Паровой ингалятор
Это прибор для вдыхания жидких лекарственных веществ в распыленном виде. Он состоит из кипятильника В, стакана К с лекарственной жидкостью и вставленной в него тонкой трубкой Т и направляющего патрубка С. Струя пара выходит из трубки кипятильника с большой скоростью. Вследствие этого давление около ее отверстия падает и лекарственная жидкость, всасываясь по трубке Т, поступает в струю, распыляется и, смешиваясь с паром, вдыхается больным через патрубок С
Водоструйный насос состоит из стеклянного сосуда Н, в который впаяно три трубки. Трубка имеет на конце коническое сужение. Насос присоединяется к водоводу и колбе К, из которой производится отсасывание. Вода, имеющая достаточно высокое давление, выходит из суженного конца трубки 1 с большей скоростью. Давление у отверстия трубки резко снижается и в сосуд А через трубку 2 засасывается воздух или жидкость, которые вместе с водой удаляются через трубку 3. Водоструйный насос удобен тем, что он не имеет вращающихся частей, требующих смазки, бесшумен и гигиеничен. Поэтому он часто применяется в лабораториях, операционных и т. п.
В уравнении Бернулли давление р называется статическим давлением рс жидкости. Оно может быть измерено обычным манометром, который двигается вместе с жидкостью, или практически при помощи неподвижной манометрической трубки, плоскость отверстия которой расположена параллельно направлению движения жидкости.
Второй член уравнения Бернулли (ρυ2/2)также имеет размерность давления и называется динамическим давлением рд в жидкости. Сумма статического и динамического давлений называется полным давлением р в жидкости:
Для измерения его применяют манометрическую трубку, изогнутую под прямым углом и помещенную отверстием навстречу движению жидкости. Частицы жидкости, заходящие в отверстие трубки полностью тормозятся в ней: скорость υ2 частиц жидкости в отверстии рав няется нулю: υ 2=0. Тогда по уравнению Бернулли
Следовательно, давление р2 в трубке:
где р1 — давление и υ1 — скорость движущейся жидкости
Если в струю жидкости поставить рядом две такие трубки, то разность уровней в трубках будет соответствовать динамическому давлению. На этом основан способ измерения скорости движения жидкости или газа В струю погружают две скрепленные вместе измерительные трубки, прямую и изогнутую (подобное устройство называется трубкой Пито), которые соединяются с U= образным манометром. Манометр покажет динамическое давление, по величине которого, пользуясь приведенной выше формулой, вычисляют искомую скорость:
Самостоятельная работа по физике Движение жидкости. Уравнение Бернулли 10 класс
Самостоятельная работа по физике Движение жидкости. Уравнение Бернулли 10 класс с ответами. Самостоятельная работа включает 5 вариантов, в каждом по 2 задания.
Вариант 1
1. По горизонтальной трубе переменного сечения течёт жидкость. Скорость течения в широкой части трубы 2 м/с. Определите скорость течения в узкой части трубы, если площади поперечного сечения этих частей трубы различаются в 1,5 раза.
2. В цилиндрическом сосуде уровень воды составляет 20 см. С какой скоростью начнёт вытекать вода, если открыть кран, установленный у основания этого сосуда?
Вариант 2
2. Скорость истечения воды из бассейна по трубе, расположенной в основании бассейна, составляет 10 м/с. Определите глубину бассейна.
Вариант 3
1. На вертикальную стену, действуя перпендикулярно, ветер оказывает давление 100 Па. Определите скорость ветра, если плотность воздуха равна 1,29 кг/м 3 .
2. Подводная лодка находится на глубине 100 м. С какой скоростью будет поступать вода в лодку, если открыть люк? Давление воздуха в лодке считайте равным атмосферному.
Вариант 4
1. Из брандспойта вертикально вверх бьёт струя воды с расходом 1 кг за 1 с. Площадь поперечного сечения у основания струи равна 1,5 см 2 . Определите площадь поперечного сечения струи на высоте 2 м.
Определите объём воды, протекающей через поперечное сечение за 1 с.
Вариант 5
1. Для смазки инструмента используется шприц с площадью поршня 1 см 2 . С какой скоростью вытекает масло (ρм = 800 кг/м 3 ) из отверстия площадью 0,6 см 2 , если на поршень действует сила 4 Н?
2. Определите высоту, на которую поднимется вода в вертикальной трубке, впаянной в узкую часть (диаметром 3 см) горизонтальной
трубы (см. рисунок), если в широкой части этой же трубы (диаметром в 3 раза большим) скорость протекания воздуха составляет 0,25 м/с.

Ответы на самостоятельную работа по физике Движение жидкости. Уравнение Бернулли 10 класс
Вариант 1
1. 3 м/с
2. 2 м/с
Вариант 2
1. В 2 раза
2. 5 м
Вариант 3
1. ≈ 6,23 м/с
2. ≈ 44,72 м/с
Вариант 4
1. 4,8 см 2
2. ≈ 2,3 л
Вариант 5
1. 12,5 м/с
2. 0,255 м
Читайте также:

