Если идеальная жидкость течет по горизонтальной трубе
Обновлено: 07.07.2024
Слободянюк А.И. Физика 10/7.11
Если по горизонтальной трубе постоянного сечения будет протекать жидкость реальная жидкость, для которой нельзя пренебречь силами вязкого трения, то давление в трубе не будет постоянным, произойдет перераспределение давления, которое будет существенно зависеть от свойств жидкости. Рассматривая проблемы возникновения сил вязкого трения, мы упоминали о такой характеристике жидкости как вязкость. Сейчас мы уточним это понятие.
Рассмотрим плоский поток жидкости, в пределах которого скорость \(
\vec \upsilon(z)\) различных слоев которого изменяется, оставаясь параллельной основанию потока (рис. 130). В реальной жидкости различные слои жидкости, имеющие разные скорости будут взаимодействовать между собой, то есть между слоями жидкости благодаря межмолекулярным взаимодействиям будут возникать силы вязкого трения – более медленный слой будет тормозить более быстрый. Важно отметить, что эти силы направлены параллельно слоям жидкости, то есть тангенциально к границе раздела (рис. 131). Величина этих сил также зависит от распределения скорости \(
\vec \upsilon(z)\) , где z - координата, ось которой направлена перпендикулярно скорости течения.
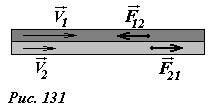
Силы вязкости определяется законом Ньютона [1] : тангенциальная сила вязкого трения между движущимися слоями жидкости приходящаяся на единицу площади соприкосновения равна
в этой формуле коэффициент пропорциональности η - полностью определяется свойствами жидкости и называется динамическим коэффициентом вязкости. Вязкость может изменяться в широких пределах, она мала для легко подвижных жидкостей, таких как вода, бензин, эфир, и велика для малоподвижных жидкостей таких как масло, мед, смола и т.д. В целом строгое понятие вязкости вполне соответствует обычным представлениям о вязких и маловязких жидкостях. Модель движущейся жидкости, в рамках которой пренебрегают вязкостью, называется идеальной жидкостью.
Обратите внимание – в случае неподвижной жидкости силы взаимодействия между слоями всегда нормальны, в движущейся жидкости появляются тангенциальные составляющие!
Важно отметить, что силы вязкости не являются консервативными, наличие этих сил, их работа приводит к переходу механической энергии в тепловую, к потерям механической энергии.
При стационарном движении жидкости трубы на нее со стороны стенок будут действовать тормозящие силы вязкого трения. Поэтому скорость движения жидкости в поперечном сечении будет различной, установится некоторое стационарное распределение скоростей – скорость максимальна в центре трубы и приближается к нулю вблизи стенок (рис. 132).
Для расчета сил вязкого трения, действующих на жидкость необходимо, прежде всего, найти распределение скоростей жидкости внутри трубы (используя закон вязкого трения), после чего можно вычислить силу сопротивления движению, расход жидкости и так далее.
Для круговой цилиндрической трубы эта задача была решена французским физиком Ж. Пуазейлем, который установил, что расход [2] жидкости пропорционален разности давлений на концах трубы Δp, четвертой степени радиуса трубы, обратно пропорционален ее длине
Q = K \frac \Delta p\) , (1)
коэффициент пропорциональности зависит от вязкости жидкости. Если поперечный профиль отличен от кругового, то формула Пуазейля несколько видоизменяется, но расход жидкости остается пропорциональным разности давлений на концах трубы
в этой формуле коэффициент пропорциональности обозначен \(
\frac\) , тогда величина R - называется гидродинамическим сопротивлением. Гидростатическое сопротивление участка трубы длиной Δl можно представить в виде R = rΔl , где r - сопротивление единицы длины трубы, зависящее от вязкости жидкости, размеров и формы поперечного сечения трубы. С увеличением площади поперечного сечения гидродинамическое сопротивление уменьшается.
Внимательно посмотрим на формулу (2) – она достойна того. Если площадь поперечного сечения трубы постоянна, то скорости движения жидкости не изменяются вдоль трубы, то есть любая частица жидкости движется с постоянной скоростью, без ускорения. Тем не менее, для того чтобы жидкость двигалась с постоянной скоростью, к ней необходимо прикладывать постоянную внешнюю силу, то есть создавать разность давлений на концах трубы. Кажущееся противоречие легко снимается, если принять во внимание силы вязкого трения, действующие между различными слоями жидкости. Фактически внешнюю силу необходимо прикладывать, чтобы преодолеть силы вязкого трения. Конечно, суммарная сила, действующая на любую часть равномерно движущейся жидкости равна нулю.
Ситуация аналогична движению тела в вязкой среде, когда на него действует сила сопротивления (рис. 133), пропорциональная скорости движения Fсопр = βυ. Если к телу приложить постоянную внешнюю силу F, то тело будет двигаться со скоростью, пропорциональной внешней приложенной силе \(
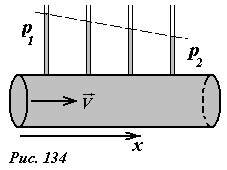
Итак, при движении вязкой жидкости по трубе внутри устанавливается распределение давлений – давление линейно падает при смещении вдоль направления движения жидкости (рис.134). Подчеркнем, что в данном случае, приложенная разность давлений является причиной движения жидкости – при стационарном движении происходит установление нужного распределения давлений вдоль трубы.
Можно сказать, что для преодоления гидростатического сопротивления R необходимо приложить разность давлений (или на сопротивлении происходит падение давления) Δp = RQ.
Направим координатную ось X вдоль трубы. Пусть в точке с координатой x = 0 давление равно p0. Применим формулу Пуазейля для слоя жидкости от x = 0 до произвольного значения координаты x. Из формулы (2) следует, что
p_0 - p(x) = QR = Qrx\) ,
где p(x) - давление жидкости в сечении с координатой x.
Таким образом, распределение давления вдоль трубы при движении вязкой жидкости представляет собой линейную зависимость p(x) = p0 - Qrx. Коэффициент наклона графика данной зависимости \(
|\frac|\) возрастает с ростом скорости течения жидкости и гидродинамического сопротивления (рис.135).
В установившемся режиме скорость [3] изменения давления вдоль трубы \(
\frac\) остается постоянной вдоль трубы. Заметим, что отношение \(
\frac\) имеет явный физический смысл. Величина F = SΔp - есть суммарная сила давления, действующая на слой жидкости толщиной Δx; следовательно, величина \(
f = \frac = \frac\) - есть суммарная сила давления, действующая на единицу объема жидкости – то есть объемная плотность силы давления.
Выделим в движущейся жидкости небольшой параллелепипед, одно из ребер которого длиной l параллельно скорости жидкости, площадь грани перпендикулярной скорости равна S (рис. 136). Пусть разность давлений между противоположными гранями этого объема равна Δp , тогда произведение ΔF = Δp'S равно суммарной силе давления на жидкость внутри выделенного объема, а величина ΔA = Δp'Sl равна работе, которую совершают силы давления внутри данного объема. Наконец, отношение \(
\frac = \Delta p\) с одной стороны разность давлений, с другой – работа сил давления, которая совершается при перетекании жидкости через данный объем.
Полученное распределение давления соответствует стационарному течению жидкости. Качественно рассмотрим процесс установления движения. Пусть длинная горизонтальная труба полностью заполнена жидкостью, с одной стороны внутри трубы расположен поршень (рис. 137). В некоторый момент времени к поршню начинают прикладывать постоянную силу. Вся жидкость в трубе сразу прийти в движение не сможет. Непосредственно перед поршнем возникнет область сжатия, которая начнет распространяться по трубе, приводя в движение все более удаленные области жидкости внутри трубы. Скорость распространения области сжатия совпадает со скоростью звука в жидкости. Наконец, по прошествии некоторого небольшого промежутка времени в трубе установится такое распределение давления, которое обеспечит постоянство скорости вдоль трубы. Именно этот установившийся режим мы и рассматриваем.
Задание для самостоятельной работы.
-
Представьте расход жидкости в виде \(
Q = \overline <\upsilon>S\) , где S - площадь поперечного сечения трубы, \(
Течение жидкости по горизонтальной трубе. Закон Пуазейля
Подходя к физическим основам системы кровообращения, рассмотрим течение вязкой, смачивающей стенки жидкости по горизонтальной трубе постоянного сечения. При относительно невысокой скорости течение имеет ламинарный характер: слой молекул, прилегающий к стенке трубы, прилипает к ней и остается неподвижным. Следующий слой молекул под действием силы давления и при противодействии силы внутреннего трения между слоями смещается относительно пристеночного слоя и движется по отношению к стенкам трубы с некоторой небольшой скоростью. Каждый последующий слой молекул, смещаясь относительно предыдущего слоя, движется по отношению к стенке трубы с постепенно возрастающей скоростью, которая достигает наибольшего значения в центре трубы.
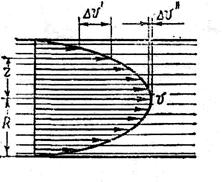
Математический анализ этого явления показывает, что распределение скоростей по сечению круглой трубы имеет параболический характер : Максимальная скорость в центре трубы . В этих формулах: — давления в начале и в конце участка трубы длиной - коэффициент вязкости
жидкости, R - радиус трубы и r- радиус рассматриваемого слоя
жидкости.
Ламинарное течение устанавливается в трубах с гладкими стенками, без резких изменений площади сечения или изгибов трубы, а так же при отсутствии множественных разветвлений. При нарушении этих условий и особенно при высоких скоростях течение переходит в турбулентное: скорости частиц жидкости при этом беспорядочно меняются, образуются местные завихрения - происходит перемешивание частиц жидкости.
Характерным для турбулентного течения являются местные изменения давления в жидкости, вызывающие колебательное движение частиц, сопровождающееся звуковыми явлениями (шум, журчание и т.п.), благодаря которым турбулентное течение легко обнаруживается. Турбулентное течение связано с дополнительными затратами энергии при движении жидкости, поэтому в кровеносной системе это может привести к дополнительной нагрузке на сердце. Шум возникающий при турбулентном течении крови, может быть использован для диагностики заболеваний. При поражении клапанов сердца возникают так называемые сердечные шумы, вызванные турбулентным течением крови. Турбулентное течение крови в аорте может быть вызвано, прежде всего, турбулентностью кровотока у входа в нее: вихри потока уже изначально существуют, когда кровь выталкивается из желудочка в аорту. У мест разветвления сосудов, а также при возрастании скорости кровотока течение может стать турбулентным и в артериях. Турбулентное течение может возникнуть в сосуде в области его локального сужения, например, при образовании тромба.
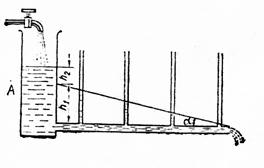
При течении реальной жидкости по горизонтальной трубе потенциальная энергия ее частиц расходуется на работу по преодолению внутреннего трения и поэтому статическое давление вдоль трубы постепенно падает. Для того чтобы обеспечить течение жидкости, необходимо в начале трубы создать давление, несколько превышающее падение давления вдоль всей трубы. В трубе постоянного сечения давление падает равномерно.
Пуазейль опытным путем установил, что средняя скорость ламинарного течения жидкости по неширокой горизонтальной круглой трубе постоянного сечения прямо пропорциональна разности давлений при входе и выходе из трубы, квадрату радиуса R трубы и обратно пропорциональна длине l трубы и коэффициенту вязкости жидкости (закон Пуазейля );
В дальнейшем, используя рассмотренный выше закон распределения скоростей по сечению трубы, Гаген вывел эту формулу теоретически.

Средняя скорость течения жидкости определяет количество жидкости Q, протекающее через поперечное сечение S трубы в единицу времени: Следовательно,
Эту формулу и называют обычно формулой Гагена — Пуазейля Ей можно придать и такой вид: , где
Величину называют гидравлическим сопротивлением. Оно обратно пропорционально четвертой степени радиуса и поэтому весьма значительно возрастает с уменьшением радиуса трубы.
Уравнение неразрывности. Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости
Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рис. 1).
Густота линии тока, характеризуемая отношением числа линий к площади перпендикулярной им площадки, через которую они проходят, больше там, где больше скорость течения жидкости, и меньше там, где скорость меньше.


Рис.1. Линии тока Рис. 2. Трубка тока
Часть жидкости, ограниченную линиями тока, называют трубкой тока.
Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются. Рассмотрим какую-либо трубку тока. Выберем два ее сечения и , перпендикулярные направлению скорости (рис.2). Если жидкость несжимаема , то произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока является величиной постоянной для данной трубки тока (уравнение неразрывности для несжимаемой жидкости), т. е.
. Уравнение Бернулли
Рис. 3. Трубка тока Аналогично, в месте сечения скорость течения ,
Рис. 3 давление и высота сечения .
Для любого сечения трубки тока идеальной жидкости выполняется следующее условие: (уравнения Бернулли).
Из уравнения Бернулли и уравнения неразрывности следует:
1) при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а в широких местах скорость меньше;
(формула Торричелли), где
- высота уровня воды над отверстием, - ускорение свободного падения.
Примеры решения задач по теме «Механика жидкости»
(Номера задач в скобках соответствуют сборнику задач по курсу физики Трофимовой Т.И.)
Задача №1(1.214). В бочку заливается вода со скоростью 200 см 3 /с. На дне бочки образовалось отверстие площадью поперечного сечения 0,8 см. Пренебрегая вязкостью воды, определите уровень воды в бочке.
Дано: =200 см 3 =2*10 -4 м3 , =1 с, = 0,8 см 2 =8*10 -5 м2 .
Скорость истечения жидкости из малого отверстия по формуле Торричелли:
- ускорение свободного падения,
- высота уровня воды в бочке над отверстием, которую можно выразить в
Для определения величины , учтем, что . Отсюда
Подставим исходные данные в полученное выражение:
Задача №2(1.225). По горизонтальной трубе в направлении, указанном на рисунке 8 стрелкой, течет жидкость. Размер уровней жидкости в манометрических трубках 1 и 2 одинакового диаметра составляет 8 см. Определите скорость течения жидкости по трубе.
Дано: = 8 см = 8*10 -2 м, .

Найти: -?
Гидростатическое давление столба жидкости в манометрических трубках уравновешивается давлением в соответствующем месте трубы, чем и определяется высота столба жидкости в этих трубках. В трубке 1 с горизонтальным срезом высота столба жидкости определяется только статическим давлением, т.е. . Трубка Пито 2 имеет срез, позволяющий воде затекать в нее, поэтому высота столба жидкости в ней определяется суммой не только статического, но и динамического давления:
Следовательно, с одной стороны .
С другой стороны .
В этих формулах - плотность жидкости, - ускорение свободного падения. Подставим исходные данные в полученное выражение:
Задача №3(1.229). Вдоль оси горизонтальной трубки диаметром 3 см, по которой течет углекислый газ, ( =7,5 кг/м 3 ) установлена трубка Пито. Пренебрегая вязкостью, определите объем газа, проходящего за 1 секунду через сечение трубы, если разность уровней в жидкостном манометре составляет =0,5 см. Плотность жидкости принять равной =1000 кг/м 3 .

Дано: =7.5 кг/м 3 , =1000 кг/м 3 , d=3 см =3*10 -2 м, =0,5 см = 5*10-2 м,

Найти:
Объем углекислого газа, протекающего за 1 секунду через сечение трубы:
Площадь поперечного сечения трубы равна . Разность уровней воды в трубке Пито обусловлена тем, что трубка 1 измеряет только статическое давление, а трубка 2 - сумму статического и динамического давления, следовательно (рис.).
С другой стороны , поэтому .
Скорость течения углекислого газа по трубе: .
Подставим выражения для величин и в выражение и получим
Подставим исходные данные в полученное выражение:
Ответ: = 2,25*10 -3 м3 .
Задача №4(1.231). Пренебрегая вязкостью жидкости, определите скорость истечения жидкости из малого отверстия в стенке сосуда, если высотауровня жидкости над отверстием составляет 1,5м.
Дано: h=1,5м.

Запишем уравнение Бернулли и уравнение неразрывности для трубки тока с сечениями S1 и S2 в виде:
Так как (отверстие малое), то из уравнения неразрывности следует, что и скоростью по сравнению со скоростью истечения жидкости из отверстия можно пренебречь.
Следовательно, и уравнение Бернулли приобретает вид:
Отсюда скорость истечения жидкости из малого отверстия выражается в виде:
Если идеальная жидкость течет по горизонтальной трубе
Движение жидкостей или газов представляет собой сложное явление. Для его описания используются различные упрощающие предположения (модели). В простейшей модели жидкость (или даже газ) предполагается несжимаемыми и идеальными (т. е. без внутреннего трения между движущимися слоями). При движении идеальной жидкости не происходит превращения механической энергии во внутреннюю, поэтому выполняется закон сохранения механической энергии. Следствием этого закона для стационарного потока идеальной и несжимаемой жидкости является уравнение Бернулли , сформулированное в 1738 г. Стационарным принято называть такой поток жидкости, в котором не образуются вихри. В стационарном потоке частицы жидкости перемещаются по неизменным во времени траекториям, которые называются линиями тока . Опыт показывает, что стационарные потоки возникают только при достаточно малых скоростях движения жидкости.
Рассмотрим стационарное движение идеальной несжимаемой жидкости по трубе переменного сечения (рис. 1.22.1). Различные части трубы могут находиться на разных высотах.
Течение идеальной жидкости по трубе переменного сечения. ; . Условие несжимаемости:За промежуток времени жидкость в трубе сечением переместится на , а в трубе сечением – на , где и – скорости частиц жидкости в трубах. Условие несжимаемости записывается в виде:
| или . |
Здесь – объем жидкости, протекшей через сечения и .
Таким образом, при переходе жидкости с участка трубы с большим сечением на участок с меньшим сечением скорость течения возрастает, т. е. жидкость движется с ускорением. Следовательно, на жидкость действует сила. В горизонтальной трубе эта сила может возникнуть только из-за разности давлений в широком и узком участках трубы. Давление в широком участке трубы должно быть больше чем в узком участке. Если участки трубы расположены на разной высоте, то ускорение жидкости вызывается совместным действием силы тяжести и силы давления. Сила давления – это упругая сила сжатия жидкости. Несжимаемость жидкости означает лишь то, что появление упругих сил происходит при пренебрежимо малом изменении объема любой части жидкости.
Так как жидкость предполагается идеальной, то она течет по трубе без трения. Поэтому к ее течению можно применить закон сохранения механической энергии.
При перемещении жидкости силы давления совершают работу:
| . |
Работа сил давления равна изменению потенциальной энергии упругой деформации жидкости, взятому с обратным знаком.
Изменения, произошедшие за время в выделенной части жидкости, заключенной между сечениями и в начальный момент времени, при стационарном течении сводятся к перемещению массы жидкости ( – плотность жидкости) из одной части трубы сечением в другую часть сечением (заштрихованные объемы на рис. 1.22.1). Закон сохранения механической энергии для этой массы имеет вид:
| , |
Это и есть уравнение Бернулли . Из него следует, что сумма
остается неизменной вдоль всей трубы. В частности, для горизонтально расположенной трубы () уравнение Бернулли принимает вид:
Величина – статическое давление в жидкости. Оно может быть измерено с помощью манометра, перемещающегося вместе с жидкостью. Практически давление в разных сечениях трубы измеряется с помощью манометрических трубок, вставленных через боковые стенки в поток жидкости, так чтобы нижние концы трубок были параллельны скоростям частиц жидкости (рис. 1.22.2). Из уравнения Бернулли следует:
Давление в жидкости, текущей по горизонтальной трубе переменного сечения, больше в тех сечениях потока, в которых скорость ее движения меньше, и наоборот, давление меньше в тех сечениях, в которых скорость больше.
Измерение давления в потоке жидкости с помощью манометров. ; Модель. Течение идеальной жидкостиЕсли сечение потока жидкости достаточно велико, то уравнение Бернулли следует применять к линиям тока , т. е. линиям, вдоль которых перемещаются частицы жидкости при стационарном течении. Например, при истечении идеальной несжимаемой жидкости из отверстия в боковой стенке или дне широкого сосуда линии тока начинаются вблизи свободной поверхности жидкости и проходят через отверстие (рис. 1.22.3).
Истечение жидкости из широкого сосудаПоскольку скорость жидкости вблизи поверхности в широком сосуде пренебрежимо мала, то уравнение Бернулли принимает вид:
где – атмосферное давление, – перепад высоты вдоль линии тока. Таким образом,
Это выражение для скорости истечения называют формулой Торричелли . Скорость истечения идеальной жидкости из отверстия в сосуде такая же, как и при свободном падении тела с высоты без начальной скорости.
В отличие от жидкостей, газы могут сильно изменять свой объем. Расчеты показывают, что сжимаемостью газов можно пренебречь, если наибольшие скорости в потоке малы по сравнению со скоростью звука в этом газе. Таким образом, уравнение Бернулли можно применять к достаточно широкому классу задач аэродинамики.
Одной из таких задач является изучение сил, действующих на крыло самолета. Строгое теоретическое решение этой задачи чрезвычайно сложно, и обычно для исследования сил применяются экспериментальные методы. Уравнение Бернулли позволяет дать лишь качественное объяснение возникновению подъемной силы крыла. На рис. 1.22.4 изображены линии тока воздуха при обтекании крыла самолета. Из-за специального профиля крыла и наличия угла атаки , т. е. угла наклона крыла по отношению к набегающему потоку воздуха, скорость воздушного потока над крылом оказывается больше, чем под крылом. Поэтому на рис. 1.22.4 линии тока над крылом располагаются ближе друг к другу, чем под крылом. Из уравнения Бернулли следует, что давление в нижней части крыла будет больше, чем в верхней; в результате появляется сила действующая на крыло. Вертикальная составляющая этой силы называется подъемной силой. Подъемная сила позволяет скомпенсировать силу тяжести, действующую на самолет, и тем самым она обеспечивает возможность полета тяжелых летательных аппаратов в воздухе. Горизонтальная составляющая представляет собой силу сопротивления среды.
Линии тока при обтекании крыла самолета и возникновение подъемной силы. – угол атакиТеория подъемной силы крыла самолета была создана Н. Е. Жуковским. Он показал, что при обтекании крыла существенную роль играют силы вязкого трения в поверхностном слое. В результате их действия возникает круговое движение ( циркуляция ) воздуха вокруг крыла (зеленые стрелки на рис. 1.22.4). В верхней части крыла скорость циркулирующего воздуха складывается со скоростью набегающего потока, в нижней части эти скорости направлены в противоположные стороны. Это и приводит к возникновению разности давлений и появлению подъемной силы.
Циркуляция воздуха, обусловленная силами вязкого трения, возникает и вокруг вращающегося тела (например, цилиндра). При вращении цилиндр увлекает прилегающие слои воздуха, вызывая его циркуляцию. Если такой цилиндр установить в набегающем потоке воздуха, то возникнет сила бокового давления, аналогичная подъемной силе крыла самолета. Это явление называется эффектом Магнуса . Рис. 1.22.5 иллюстрирует обтекание вращающегося цилиндра набегающим потоком. Эффект Магнуса проявляется, например, при полете закрученного мяча при игре в теннис или футбол.
Обтекание вращающегося цилиндра набегающим потоком воздухаИтак, во многих явлениях аэродинамики существенную роль играют силы вязкого трения. Они приводят к возникновению циркулирующих потоков воздуха вокруг крыла самолета или вокруг вращающегося тела, к появлению силы сопротивления среды и т. д. Уравнение Бернулли не учитывает сил трения. Его вывод основан на законе сохранения механической энергии при течении жидкости или газа. Поэтому с помощью уравнения Бернулли нельзя дать исчерпывающего объяснения явлений, в которых проявляются силы трения. В этих случаях можно руководствоваться только качественными соображениями – чем больше скорость, тем меньше давление в потоке газа.
Коэффициент пропорциональности в этой формуле зависит от свойств жидкости.
Поэтому, если тяжелый шарик бросить в высокий сосуд, наполненный вязкой жидкостью (например, глицерином), то через некоторое время скорость шарика достигнет установившегося значения, которое не будет изменяться при дальнейшем движении шарика. При движении с установившейся скоростью силы, действующие на шарик (сила тяжести выталкивающая сила и сила сопротивления среды оказываются скомпенсированными, и их равнодействующая равна нулю.
Если идеальная жидкость течет по горизонтальной трубе
В этом параграфе мы применим закон сохранения энергии к движению жидкости или газа по трубам. Движение жидкости по трубам часто встречается в технике и быту. По трубам водопровода подается вода в городе в дома, к местам ее потребления. В машинах по трубам поступает масло для смазки, топливо в двигатели и т. д. Движение жидкости по трубам нередко встречается и в природе. Достаточно сказать, что кровообращение животных и человека — это течение крови по трубкам — кровеносным сосудам. В какой-то мере течение воды в реках тоже является разновидностью течения жидкости по трубам. Русло реки — это своеобразная труба для текущей воды.
Как известно, неподвижная жидкость в сосуде согласно закону Паскаля передает внешнее давление по всем направлениям и во все точки объема без изменения. Однако, когда жидкость течет без трения по трубе, площадь поперечного сечения которой на разных участках различна, давление оказывается неодинаковым вдоль трубы. Выясним, почему давление в движущейся жидкости зависит от площади поперечного сечения трубы. Но сначала ознакомимся с одной важной особенностью всякого потока жидкости.
Предположим, что жидкость течет по горизонтально расположенной трубе, сечение которой в разных местах различное, например по трубе, часть которой показана на рисунке 207.
Если бы мы мысленно провели несколько сечений вдоль трубы, площади которых соответственно равны и измерили бы количество жидкости, протекающей через каждое из них за какой-то промежуток времени то мы обнаружили бы, что через каждое сечение протекло одно и то же количество жидкости. Это значит, что вся та жидкость, которая за время проходит через первое сечение, за такое же время проходит и через третье сечение, хотя оно по площади значительно меньше, чем первое. Если бы это было не так и через сечение площадью за время проходило, например, меньше жидкости, чем через сечение площадью то избыток жидкости должен был бы где-то накапливаться. Но жидкость заполняет всю трубу, и накапливаться ей негде.
Как же может жидкость, протекшая через широкое сечение, успеть за такое же время «протиснуться» через узкое? Очевидно, что для этого при прохождении узких частей трубы скорость движения должна быть больше, и как раз во столько раз, во сколько раз площадь сечения меньше.
Действительно, рассмотрим некоторое сечение движущегося столба жидкости, совпадающее в начальный момент времени с одним из сечений трубы (рис. 208). За время эта площадка переместится на расстояние которое равно где — скорость течения жидкости. Объем V жидкости, протекшей через сечение трубы, равен произведению площади этого сечения на длину
В единицу же времени протекает объем жидкости —
Объем жидкости, протекающей в единицу времени через сечение трубы, равен произведению площади поперечного сечения трубы на скорость течения.
Как мы только что видели, этот объем должен быть одним и тем же в разных сечениях трубы. Поэтому, чем меньше сечение трубы, тем больше скорость движения.
Сколько жидкости проходит через одно сечение трубы за некоторое время, столько же ее должно пройти за такое
же время через любое другое сечение.
При этом мы считаем, что данная масса жидкости всегда имеет один и тот же объем, что она не может сжаться и уменьшить свой объем (о жидкости говорят, что она несжимаема). Хорошо известно, например, что в узких местах реки скорость течения воды больше, чем в широких. Если обозначить скорость течения жидкости в сечениях площадями через то можно написать:
Отсюда видно, что при переходе жидкости с участка трубы с большей площадью сечения на участок с меньшей площадью сечения скорость течения увеличивается, т. е. жидкость движется с ускорением. А это по второму закону Ньютона означает, что на жидкость действует сила. Что это за сила?
Этой силой может быть только разность между силами давления в широком и узком участках трубы. Таким образом, в широком участке давление жидкости должно быть больше, чем в узком участке трубы.
Это же следует из закона сохранения энергии. Действительно, если в узких местах трубы увеличивается скорость движения жидкости, то увеличивается и ее кинетическая энергия. А так как мы приняли, что жидкость течет без трения, то этот прирост кинетической энергии должен компенсироваться уменьшением потенциальной энергии, потому что полная энергия должна оставаться постоянной. О какой же потенциальной энергии здесь идет речь? Если труба горизонтальна, то потенциальная энергия взаимодействия с Землей во всех частях трубы одна и та же и не может измениться. Значит, остается только потенциальная энергия упругого взаимодействия. Сила давления, которая заставляет жидкость течь по трубе, — это и есть упругая сила сжатия жидкости. Когда мы говорим, что жидкость несжимаема, то имеем лишь в виду, что она не может быть сжата настолько, чтобы заметно изменился ее объем, но очень малое сжатие, вызывающее появление упругих сил, неизбежно происходит. Эти силы и создают давление жидкости. Вот это сжатие жидкости и уменьшается в узких частях трубы, компенсируя рост скорости. В узких местах труб давление жидкости должно быть поэтому меньше, чем в широких.
В этом состоит закон, открытый петербургским академиком Даниилом Бернулли:
Давление текущей жидкости больше в тех сечениях потока, в которых скорость ее движения меньше, и,
наоборот, в тех сечениях, в которых скорость больше, давление меньше.
Как это ни покажется странным, но когда жидкость «протискивается» через узкие участки трубы, то ее сжатие не увеличивается, а уменьшается. И опыт хорошо это подтверждает.
Если трубу, по которой течет жидкость, снабдить впаянными в нее открытыми трубками — манометрами (рис. 209), то можно будет наблюдать распределение давления вдоль трубы. В узких местах трубы высота столба жидкости в манометрической трубке меньше, чем в широких. Это означает, что в этих местах давление меньше. Чем меньше сечение трубы, тем больше в ней скорость течения и меньше давление. Можно, очевидно, подобрать такое сечение, в котором давление равно внешнему атмосферному давлению (высота уровня жидкости в манометре будет тогда равна нулю). А если взять еще меньшее сечение, то давление жидкости в нем будет меньше атмосферного.
Такой поток жидкости можно использовать для откачки воздуха. На этом принципе действует так называемый водоструйный насос. На рисунке 210 изображена схема такого насоса. Струю воды пропускают через трубку А с узким отверстием на конце. Давление воды у отверстия трубы меньше атмосферного. Поэтому
газ из откачиваемого объема через трубку В втягивается к концу трубки А и удаляется вместе с водой.
Все сказанное о движении жидкости по трубам относится и к движению газа. Если скорость течения газа не слишком велика и газ не сжимается настолько, чтобы изменялся его объем, и если, кроме того, пренебречь трением, то закон Бернулли верен и для газовых потоков. В узких частях труб, где газ движется быстрее, давление его меньше, чем в широких частях, и может стать меньше атмосферного. В некоторых случаях для этого даже не требуется трубы.
Можно проделать простой опыт. Если дуть на лист бумаги вдоль его поверхности, как показано на рисунке 211, можно увидеть, что бумага станет подниматься вверх. Это происходит из-за понижения давления в струе воздуха над бумагой.
Такое же явление имеет место при полете самолета. Встречный поток воздуха набегает на выпуклую верхнюю поверхность крыла летящего самолета, и за счет этого происходит понижение давления. Давление над крылом оказывается меньше, чем давление под крылом. Именно поэтому возникает подъемная сила крыла.
Упражнение 62
1. Допустимая скорость течения нефти по трубам равна 2 м/сек. Какой объем нефти проходит через трубу диаметром 1 м в течение 1 ч?
2. Измерьте количество воды, вытекающей из водопроводного крана за определенное время Определите скорость течения воды, измерив диаметр трубы перед краном.
3. Каким должен быть диаметр трубопровода, по которому должно протекать воды в час? Допустимая скорость течения воды 2,5 м/сек.
Если идеальная жидкость течет по горизонтальной трубе
Трение жидкости. Для измерения статического давления жидкости, текущей в трубе, можно применить такое устройство: к маленьким отверстиям, просверленным в трубе, присоединяют вертикальные открытые сверху трубочки ( манометрические трубки, рис. 307). Если жидкость в трубе находится под давлением, то в вертикальной трубочке жидкость поднимается на высоту, соответствующую статическому давлению в данном месте трубы ). В самом деле, небольшое отверстие почти не внесет изменений в поток жидкости, текущей в трубе. Устанавливая манометрические, трубки в разных местах трубы, мы сможем измерить статическое давление в соответственных точках.

Рис. 307. Манометрические трубки показывают статическое давление в трубе, по которой течет жидкость
Исследуем при помощи манометрических трубок статическое давление жидкости, текущей вдоль трубы постоянного сечения. Для этого воспользуемся прибором, изображенным на рис. 308. По высоте воды в манометрических трубках, расположенных вдоль трубы, мы можем определить статическое давление в разных местах трубы. Опыт показывает, что вдоль трубы по течению давление падает: чем дальше от начала трубы, тем меньше статическое давление текущей жидкости. При этом в узких трубах давление падает быстрее, чем в широких. В достаточно широких и коротких трубах при не очень большой скорости течения падение давления практически незаметно.

Рис. 308. Манометрические трубки показывают падение давления вдоль трубы, по которой течет вода
Падение давления жидкости в трубе объясняется трением. На жидкость, текущую по трубе, действуют со стороны стенок трубы силы трения; они направлены противоположно движению жидкости. Выделим мысленно в трубе объем жидкости (рис. 309). Со стороны стенок трубы на выделенный объем действуют силы трения . Если жидкость течет по трубе равномерно (с постоянной скоростью), то силы давления, действующие на выделенный объем, должны уравновешивать силы трения. Отсюда заключаем, что сила давления действующая в направлении движения, по модулю должна быть больше силы давления , действующей в противоположном направлении. Поэтому давление на задней поверхности выделенного объема должно быть больше давления на передней поверхности , т. е. давление должно убывать вдоль трубы по течению.

Рис. 309. Сумма сил давления и уравновешивает силы трения со стороны стенок трубы
Если увеличить скорость жидкости, текущей по трубе, то сила трения возрастет. Поэтому при быстром течении жидкости падение давления в данной трубе больше, чем при медленном течении. При данной скорости течения трение сказывается сильнее в узких трубах, чем в широких; поэтому вдоль узких труб давление падает быстрее.
При устройстве водопроводов необходимо учитывать падение давления в водопроводных трубах. Когда все краны водопровода закрыты и вода по трубам не течет, то давление воды соответствует высоте водонапорной башни (§ 155). В покоящейся жидкости никаких сил трения не возникает. Если же краны открыты и вода течет, то трение в трубах вызывает падение давления: «напор» воды уменьшается. Чем большее число кранов открыто и чем быстрее течет вода, тем больше падает напор.
При недостаточной высоте водонапорной башни может оказаться, что падение давления воды в трубах больше, чем давление, соответствующее высоте башни над верхними этажами дома. Тогда вода перестанет течь из кранов верхних этажей. Но в часы, когда потребление воды невелико, потери давления уменьшаются и вода в верхних этажах появляется снова; и, вообще, давление воды в водонапорной сети больше всего ночью, когда расход воды мал, скорость движения воды по трубам мала, и поэтому трение сравнительно невелико.
Падение давления в водопроводе демонстрируется на следующей модели (рис. 310). Узкая (для увеличения трения) труба и ее ответвление , снабженные манометрическими трубками, могут закрываться кранами и . Если налить воду в сосуд и закрыть краны, то давление в трубах и будет соответствовать высоте налитой воды и вода во всех манометрических трубках будет стоять на том же уровне, что и в сосуде . Если немного открыть кран , то в трубе мы увидим знакомую уже нам картину падения давления вдоль трубы; в трубе давление упадет, но будет одинаково во всех точках и равно давлению в точке . Если больше открыть кран , то и падение давления вдоль трубы станет больше. Если приоткрыть еще кран , то появится падение давления воды вдоль трубы и одновременно уменьшится давление во всех точках трубы .
Т. Движение жидкостей
Зависимость давления жидкости от скорости ее течения
В предыдущих параграфах были рассмотрены законы равновесия жидкостей и газов. Теперь рассмотрим некоторые явления, связанные с их движением.
Движение жидкости называют течением, а совокупность частиц движущейся жидкости потоком. При описании движения жидкости определяют скорости, с которыми частицы жидкости проходят через данную точку пространства. Если в каждой точке пространства, заполненного движущейся жидкостью, скорость не изменяется со временем, то такое движение называется установившимся, или стационарным. При стационарном течении любая частица жидкости проходит через данную точку пространства с одним и тем же значением скорости. Мы будем рассматривать только стационарное течение идеальной несжимаемой жидкости. Идеальной называют жидкость, в которой отсутствуют силы трения.
Как известно, неподвижная жидкость в сосуде, согласно закону Паскаля, передает внешнее давление ко всем точкам жидкости без изменения. Но когда жидкость течет без трения по трубе переменного поперечного сечения, давление в разных местах трубы неодинаково. Оценить распределение давлений в трубе, по которой течет жидкость, можно с помощью установки, схематически изображенной на рисунке 1. Вдоль трубы впаивают вертикальные открытые трубки-манометры. Если жидкость в трубе находится под давлением, то в манометрической трубке жидкость поднимается на некоторую высоту, зависящую от давления в данном месте трубы. Опыт показывает, что в узких местах трубы высота столбика жидкости меньше, чем в широких. Это значит, что в этих узких местах давление меньше. Чем это объясняется?
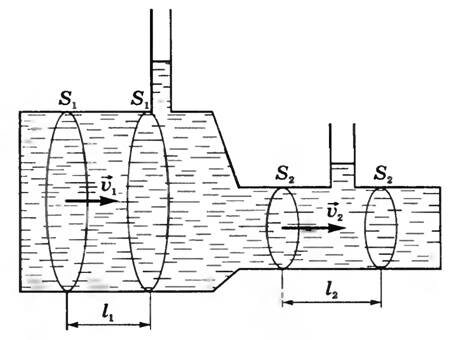
Предположим, что несжимаемая жидкость течет по горизонтальной трубе с переменным сечением (рис. 1). Выделим мысленно несколько сечений в трубе, площади которых обозначим S1 и S2. При стационар ном течении через любое поперечное сечение трубы за равные промежутки времени переносятся одинаковые объемы жидкости.
Пусть υ1 — скорость жидкости через сечение S1, υ2 — скорость жидкости через сечение S2. За время Δt объемы жидкостей, протекающих через эти сечения, будут равны:
\begin \Delta V_1 = l_1S_1 = \upsilon_1 \Delta t_1 \cdot S_1 ; \\ \Delta V_2 = l_2S_2 = \upsilon_2 \Delta t_2 \cdot S_2 . \end\)
Так как жидкость несжимаема, то ΔV1 = ΔV2. Следовательно, υ1S1 = υ2S2 или υS = const для несжимаемой жидкости. Это соотношение называется уравнением неразрывности.
Из этого уравнения \(
\frac<\upsilon_1> <\upsilon_2>= \frac\) , т.е. скорости жидкости в двух любых сечениях обратно пропорциональны площадям сечений. Это значит, что частицы жидкости при переходе из широкой части трубы в узкую ускоряются. Следовательно, на жидкость, поступающую в более узкую часть трубы, действует со стороны жидкости, еще находящейся в широкой части трубы, некоторая сила. Такая сила может возникнуть только за счет разности давлений в различных частях жидкости. Так как сила направлена в сторону узкой части трубы, то в широком участке трубы давление должно быть больше, чем в узком. Учитывая уравнение неразрывности, можно сделать вывод: при стационарном течении жидкости давление меньше в тех местах, где больше скорость течения, и, наоборот, больше в тех местах, где скорость течения меньше.
К этому выводу впервые пришел Д. Бернулли, поэтому данный закон называют законом Бернулли.
Применение закона сохранения энергии к потоку движущейся жидкости позволяет получить уравнение, выражающее закон Бернулли (приводим без вывода)\[
p_1 + \frac = p_2 + \frac\] — уравнение Бернулли для горизонтальной трубки.
Здесь p1 и p2 — статические давления, ρ — плотность жидкости. Статическое давление равно отношению силы давления одной части жидкости на другую к площади соприкосновения, когда скорость их относительного движения равна нулю. Такое давление измерил бы манометр, движущийся вместе с потоком. Неподвижная монометрическая трубка с отверстием, обращенным навстречу потоку, измерит давление \(
\frac\) имеют, с одной стороны, размерность давления, с другой — размерность объемной плотности энергии, т. е. энергии, приходящейся на единицу объема. Действительно, \(
W_k = \frac\), масса жидкости m = ρV. Если V = 1 м 3 , то \(
\frac\) — называют динамическим давлением. Это кинетическая энергия потока в единичном объеме жидкости (объемная плотность энергии).
Если трубка не горизонтальная, то надо учитывать и гидростатическое давление жидкости. Уравнение Бернулли будет иметь вид:
где h1 и h2 — высоты, на которых находятся сечения S1 и S2.
Закон Бернулли лежит в основе принципа действия многих технических устройств и приборов: водоструйного насоса, пульверизатора, форсунки карбюратора. Закон Бернулли позволяет объяснить возникновение подъемной силы крыла самолета.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 106-108.
Читайте также:

